Lo scarto quadratico medio
Lo scarto quadratico medio, o deviazione standard, è una misura statistica della dispersione dei dati rispetto alla media di un insieme di valori ossia dell'incertezza. Si calcola come la radice quadrata della media dei quadrati degli scarti di ciascun dato dal valore medio.
$$ \sigma = \sqrt{\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \ldots + (x_N - \bar{x})^2}{N}} $$
Dove \( x_i \) è ciascuna misura, \( \bar{x} \) è il valore medio, \( N \) è il numero totale di misure.
Quando devi gestire una serie di misure sperimentali composta da molti valori, lo scarto quadratico medio (devianza standard) ti consente di quantificare l'incertezza in modo più preciso.
Questo indicatore rappresenta l'incertezza delle misurazioni e indica quanto i valori si distribuiscono intorno alla media: più è piccolo, maggiore è la precisione delle misure.
Un esempio
Ad esempio, supponi di avere cinque misurazioni di tempo (in secondi) prese per un esperimento.
$$ 20.5, \ 21.0, \ 21.5, \ 22.0, \ 20.0 \ s $$
Usando il metodo della semidispersione, per calcolare l'errore assoluto avresti semplicemente considerato gli estremi
$$ e_x = \frac{22.0-20.0}{2} = 1 \ s $$
Si tratta però di una stima che non considera tutte le misurazioni. E' quindi molto approssimativa.
Per avere una misura dell'incertezza migliore, puoi calcolare la devianza standard.
Prima di tutto, calcola la media (\(\bar{x}\)) dei valori delle misurazioni.
$$ \bar{x} = \frac{20.5 + 21.0 + 21.5 + 22.0 + 20.0}{5} = \frac{105.0}{5} = 21.0 \, \text{secondi} $$
Poi calcola ora lo scarto di ciascuna misura rispetto alla media, sottraendo il valore medio da ciascuna misura:
- \(20.5 - 21.0 = -0.5\)
- \(21.0 - 21.0 = 0.0\)
- \(21.5 - 21.0 = 0.5\)
- \(22.0 - 21.0 = 1.0\)
- \(20.0 - 21.0 = -1.0\)
Quindi, gli scarti sono: \(-0.5, 0.0, 0.5, 1.0, -1.0\).
Nota che se calcolassimo la media degli scarti, otterremmo zero, poiché scarti positivi e negativi si compensano. $$ \frac{(-0.5)+0.0+0.5+1.0+(-1.0)}{5} = \frac{0}{5} $$ Per evitarlo, eleviamo ciascuno scarto al quadrato, rendendoli tutti positivi, e calcoliamo la media di questi quadrati. Infine, estraiamo la radice quadrata per ottenere lo scarto quadratico medio nell’unità di misura originale.
Eleva al quadrato ogni scarto per eliminare i segni negativi.
- \((-0.5)^2 = 0.25\)
- \((0.0)^2 = 0.0\)
- \((0.5)^2 = 0.25\)
- \((1.0)^2 = 1.0\)
- \((-1.0)^2 = 1.0\)
I quadrati degli scarti sono quindi: \(0.25, 0.0, 0.25, 1.0, 1.0\).
Somma questi valori e dividi per il numero di misure (5) per ottenere la media dei quadrati degli scarti.
$$ \text{media dei quadrati degli scarti} = \frac{0.25 + 0.0 + 0.25 + 1.0 + 1.0}{5} = \frac{2.5}{5} = 0.5 $$
Infine, per ottenere lo scarto quadratico medio (σ), calcola la radice quadrata della media dei quadrati degli scarti.
$$ \sigma = \sqrt{0.5} \approx 0.71 \, \text{secondi} $$
Il risultato, \( \sigma \approx 0.71 \) secondi, rappresenta lo scarto quadratico medio (devianza standard) della serie di misurazioni.
$$ x = \bar{x} \pm \sigma $$
In questo caso la media è $ \bar{x} = 21 \ s $ e $ \sigma = 0.71 \ s $
$$ x = 21.0 \pm 0.71 \ \text{sec} $$
Questo valore ti indica con maggiore precisione quanto le misurazioni sono distribuite intorno alla media di \(21.0\) secondi.
Più lo scarto quadratico medio è basso, più le misurazioni sono vicine alla media e, quindi, più precise.
La deviazione standard non è solo una misura dell'incertezza, ma anche uno strumento fondamentale per applicare la curva di Gauss nella rappresentazione dei dati. Grazie alla deviazione standard, possiamo prevedere la probabilità con cui i valori si distribuiscono attorno alla media in una distribuzione normale.
La curva di Gauss e la distribuzione normale
In statistica, quando raccogliamo un numero sufficientemente grande di misure affette da errori casuali, questi tendono a distribuirsi secondo una forma caratteristica, nota come curva di Gauss o distribuzione normale.
La curva di Gauss ha una forma a campana simmetrica attorno al valore medio e descrive la probabilità di ottenere una misura con un determinato scarto dalla media.
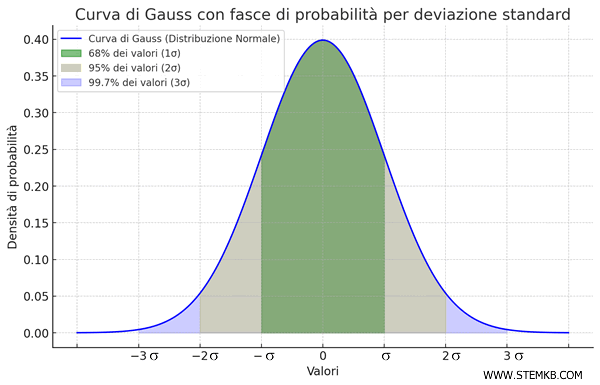
In una distribuzione normale:
- Circa il 68% dei valori si trova entro una deviazione standard (σ) dalla media,
- Circa il 95% entro due deviazioni standard,
- Circa il 99.7% entro tre deviazioni standard.
Questa proprietà rende la curva di Gauss un modello universale per descrivere l'incertezza in una moltitudine di fenomeni naturali e sperimentali, dalla fisica alla biologia, fino all’economia.
Esempio.Supponi di avere una media di 20.5 secondi e una deviazione standard di 0.3 secondi, su un totale di 1000 misurazioni. Con questi dati puoi stimare che:
- Il 68% dei valori si trova entro una deviazione standard (σ) dalla media, circa 680 misurazioni rientrano nell'intervallo tra 20.2 e 20.8 secondi.
- Il 95% dei valori si trova entro due deviazione standard (2σ) dalla media, circa 950 misurazioni rientrano nell'intervallo tra 19.9 e 21.1 secondi.
- Il 99.7% dei valori si trova entro tre deviazione standard (2σ) dalla media, circa 950 misurazioni rientrano nell'intervallo tra 19.6 e 21.4 secondi.
Questi intervalli rappresentano la distribuzione attesa delle misurazioni intorno alla media, con una copertura progressivamente maggiore per ciascuna fascia di deviazioni standard.
Quindi, lo scarto quadratico medio non è solo una misura matematica, ma anche uno strumento cruciale per interpretare la distribuzione dei dati intorno alla media.