L'ordine di grandezza in fisica
L’ordine di grandezza (odg) di un numero è la potenza di 10 più vicina a quel numero. Per determinare l'odg, si converte il numero in notazione scientifica, cioè nella forma \( a \times 10^n \), dove \( a \) è un numero compreso tra 1 e 10, e \( n \) è l’esponente della potenza di 10.
In pratica, l'ordine di grandezza si ottiene seguendo una semplice regola:
- Se \( a \) è inferiore a 5, si considera l’odg come \( 10^n \);
- Se \( a \) è pari o superiore a 5, si arrotonda aggiungendo 1 all’esponente, ottenendo quindi \( 10^{n+1} \).
Questa semplificazione permette di avere un’idea della "dimensione" del numero senza doverne conoscere il valore esatto.
L’ordine di grandezza è un concetto utile per comprendere la dimensione di una misura, specialmente quando si tratta di valori molto grandi o molto piccoli, piuttosto che concentrarsi sul valore esatto della misura stessa. In molti contesti è sufficiente approssimarla per capire in quale intervallo numerico si trova, cioè in quale “potenza di dieci” si colloca. Questo ti permette di ottenere una stima rapida, facilita la comprensione e il confronto tra numeri molto diversi.
L’ordine di grandezza si applica in diversi contesti, dalla fisica all'economia, e aiuta a comunicare e comparare grandezze molto diverse.
Esempio
Vediamo qualche esempio pratico per chiarire il concetto:
| Numero | Notazione scientifica | Odg | Spiegazione |
|---|---|---|---|
| 360 | 3,6·102 | 102 | Il numero 360 in notazione scientifica è \( 3,6 \times 10^2 \). Poiché 3,6 è minore di 5, l’ordine di grandezza di 360 è \( 10^2 \). |
| 9200 | 9,2·103 | 104 | Il numero 9200 in notazione scientifica è \( 9,2 \times 10^3 \). Dato che 9,2 è maggiore di 5, si arrotonda aggiungendo 1 all’esponente, per cui l’ordine di grandezza di 9200 è \( 10^4 \). |
| 0,00042 | 4,2·10-4 | 10-4 | Il numero 0,00042 in notazione scientifica è \( 4,2 \times 10^{-4} \). Poiché 4,2 è minore di 5, l’odg è \( 10^{-4} \). |
| 580 | 5,8·102 | 103 | Il numero 580 in notazione scientifica è \( 5,8 \times 10^2 \). Poiché 5,8 è maggiore di 5, si arrotonda a \( 10^3 \) come odg. |
| 0,0072 | 7,2·10-3 | 10-2 | Il numero 0,0072 in notazione scientifica è \( 7,2 \times 10^{-3} \). Dato che 7,2 è maggiore di 5, si somma 1 all’esponente e l’odg è \( 10^{-2} \). |
| 12500 | 1,25·104 | 104 | Il numero 12500 in notazione scientifica è \( 1,25 \times 10^4 \). Poiché 1,25 è minore di 5, l’odg è \( 10^4 \). |
| 0,000056 | 5,6·10-5 | 10-4 | Il numero 0,000056 in notazione scientifica è \( 5,6 \times 10^{-5} \). Poiché 5,6 è maggiore di 5, si somma 1 all’esponente e l’odg è \( 10^{-4} \). |
| 475 | 4,75·102 | 102 | Il numero 475 in notazione scientifica è \( 4,75 \times 10^2 \). Poiché 4,75 è minore di 5, l’odg è \( 10^2 \). |
| 21000 | 2,1·104 | 104 | Il numero 21000 in notazione scientifica è \( 2,1 \times 10^4 \). Poiché 2,1 è minore di 5, l’odg è \( 10^4 \). |
| 680000 | 6,8·105 | 106 | Il numero 680000 in notazione scientifica è \( 6,8 \times 10^5 \). Poiché 6,8 è maggiore di 5, si somma 1 all’esponente e l’odg è \( 10^6 \). |
Questi esempi mostrano come l’odg permetta di comprendere rapidamente quanto siano grandi o piccole certe quantità.
Un’eccezione: i numeri tra 5 e 5,5
Esiste una zona “grigia” per i numeri tra 5 e 5,5 in cui per convenzione si prende la potenza di dieci con esponente superiore anche se non è la più vicina.
Ad esempio, considera il numero 510. In notazione scientifica, possiamo scriverlo come $$ 5,1 \times 10^2 $$ Secondo la regola generale, siccome il numero decimale è maggiore o uguale a 5, consideriamo l’ordine di grandezza come \( 10^3 \). Tuttavia, se osservi con attenzione le distanze di \( 510 \) da \( 10^2 \) e \( 10^3 \) ti puoi rendere conto che la potenza più vicina è \( 10^ 2 \).
- \( |10^2-510| = |100-510| = 410 \)
- \( |10^3-510| = |1000-510| = 490 \)
Sulla linea dei numeri, 510 è effettivamente più vicino a 100 (che corrisponde a \( 10^2 \)) che a 1000 (\( 10^3 \)).
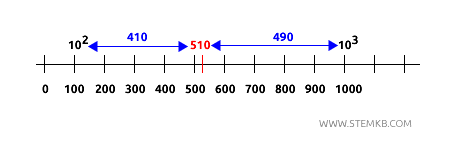
Questa discrepanza si verifica solo per valori di \( a \) compresi tra 5 e 5,5, e si può risolvere valutando caso per caso.
In questi casi, per convenzione si considera comunque la potenza di 10 superiore anche se non è la più vicina.