Volume
Il volume è una grandezza fisica che misura la quantità di spazio occupata da un corpo, una sostanza o una porzione di spazio. Si calcola come il prodotto delle dimensioni nelle tre direzioni principali (lunghezza, larghezza e altezza). $$ V = [L] \cdot [L] \cdot [L] $$
Nel sistema internazionale (SI) il volume si esprime comunemente in unità cubiche, come il metro cubo (\(\text{m}^3\)).
E' una misura fondamentale che descrive la quantità di spazio occupata da un oggetto, un liquido o una porzione di spazio.
Ad esempio, immagina di dover riempire una scatola: il volume ci dice quanta capacità ha quella scatola, o quanta materia può contenere.
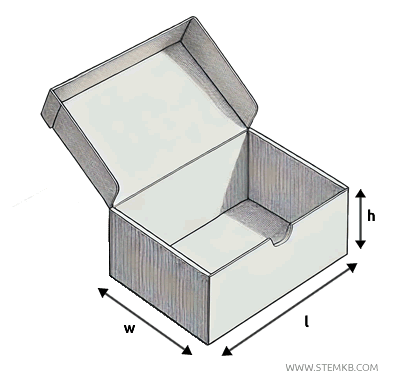
Il volume viene calcolato moltiplicando le dimensioni dello spazio considerato, tipicamente in tre direzioni: lunghezza (l), larghezza (w) e altezza (h).
Comprendere come calcolare e convertire tra diverse unità di volume ci permette di affrontare problemi quotidiani con più consapevolezza e precisione. Che si tratti di riempire un bicchiere d’acqua o di misurare il volume di una stanza, sapere come il volume si esprime e si misura è uno strumento fondamentale per navigare il mondo che ci circonda.
Un esempio di calcolo del volume
Prendiamo ad esempio un parallelepipedo (come una scatola rettangolare).

Per calcolare il suo volume, si moltiplicano le tre lunghezze dei suoi spigoli:
$$ \text{Volume} = \text{lunghezza} \times \text{larghezza} \times \text{altezza} $$
Se consideriamo un parallelepipedo con lunghezza di 8 metri, larghezza di 4 metri e altezza di 4 metri, il volume risulta:
$$ \text{Volume} = (8\,\text{m}) \times (4\,\text{m}) \times (4\,\text{m}) = 128\,\text{m}^3 $$
Ciò significa che questo solido occupa uno spazio equivalente a 128 cubi di un metro per lato.
Esempio 2
Per capire meglio la relazione tra volume e unità di misura più piccole, prendiamo un esempio concreto: il cubo di Rubik.
Nella sua versione classica, il cubo di Rubik ha uno spigolo di 5,4 cm.
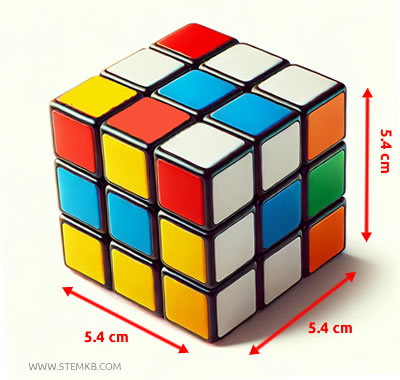
Il volume totale del cubo può essere calcolato come:
$$ \text{Volume} = (5,4\,\text{cm}) \times (5,4\,\text{cm}) \times (5,4\,\text{cm}) = 157,464\,\text{cm}^3 $$
Inoltre, il cubo è composto da 26 cubetti più piccoli, ognuno con spigoli di 1,8 cm.
Anche per questi piccoli cubi si può calcolare facilmente il volume:
$$ \text{Volume del cubetto} = (1,8\,\text{cm})^3 = 5,832\,\text{cm}^3 $$
Le unità di misura del volume
L'unità principale del volume è il metro cubo (\(\text{m}^3\)), che rappresenta il volume di un cubo con spigoli lunghi 1 metro.
Tuttavia, in situazioni quotidiane, spesso si utilizzano altre unità come il litro (L) o il millilitro (mL), che sono più pratiche per misurare volumi di liquidi.
Per fare un confronto diretto con il metro cubo, un litro è definito come un decimetro cubo (\(1\,\text{dm}^3\)).
$$ 1\,\text{L} = 1\,\text{dm}^3 = 0,001\,\text{m}^3 $$
In altre parole, un metro cubo equivale a 1000 litri:
$$ 1\,\text{m}^3 = 1000\,\text{L} $$
Questa equivalenza ci aiuta a convertire facilmente tra le due unità, rende più semplice calcolare e confrontare volumi in contesti diversi, come quelli scientifici o nella vita di tutti i giorni.
Ad esempio, quando leggiamo le etichette delle bottiglie d'acqua il volume è espresso in litri.
Un'altra unità utile per descrivere piccoli volumi è il millilitro (mL), che equivale a un centimetro cubo (\(\text{cm}^3\)). Quindi, 1 mL è esattamente pari al volume di un cubetto con spigolo di 1 cm:
$$ 1\,\text{mL} = 1\,\text{cm}^3 $$
Questo sottomultiplo del litro è particolarmente utile quando si misura la capacità di piccoli contenitori o quando si lavora con sostanze liquide in laboratorio.
Le conversioni dell'unità di misura in multipli o sottomultipli
Quando effettui delle conversioni tra unità di volume, ti consiglio di ricordare la scala dei prefissi del Sistema Internazionale e tenere a mente che nel caso del volume le conversioni coinvolgono l'elevazione al cubo (es. 10³, 100³, 1000³) perché stai lavorando con misure tridimensionali.
Questo rende le conversioni tra le diverse unità di misura un po' più complesse rispetto alle unità di lunghezza o superficie, ma con un po' di pratica diventa un processo semplice e intuitivo.
Quindi, ogni conversione implica una variazione che tiene conto delle tre dimensioni (larghezza, altezza e profondità).
Vediamo alcune conversioni principali:
1] Da metri cubi (m³) a decimetri cubi (dm³)
Un metro cubo (1 m³) corrisponde a 1000 decimetri cubi (dm³). Questo perché in ogni lato del cubo ci sono 10 decimetri (1 m = 10 dm), e quindi:
$$ 1 \text{m}^3 = 10 \text{dm} \times 10 \text{dm} \times 10 \text{dm} = 10^3 \text{dm}^3 = 1000 \text{dm}^3 $$
Il decimetro cubo è comunemente utilizzato per misurare i volumi dei liquidi ed è spesso indicato come litro (L), quindi 1 dm³ = 1 L.
2] Da metri cubi (m³) a centimetri cubi (cm³)
Un metro cubo (1 m³) equivale a 1.000.000 di centimetri cubi (cm³). Questo perché un metro contiene 100 centimetri (1 m = 100 cm), e quindi:
$$ 1 \text{m}^3 = 100 \text{cm} \times 100 \text{cm} \times 100 \text{cm} = 1.000.000 \text{cm}^3 $$
Puoi utilizzare la conversione anche usando la notazione esponenziale su base dieci
$$ 1 \text{m}^3 = 10^2 \text{cm} \times 10^2 \text{cm} \times 10^2 \text{cm} = (10^2)^3 \text{cm}^3 = 10^6 \text{cm}^3 $$
Il centimetro cubo è spesso utilizzato in contesti dove si misura il volume di piccoli oggetti o di campioni di liquidi.
3] Da metri cubi (m³) a millimetri cubi (mm³)
Per passare dai metri cubi ai millimetri cubi, si considera che in un metro ci sono 1000 millimetri (1 m = 1000 mm):
$$ 1 \text{m}^3 = 1000 \text{mm} \times 1000 \text{mm} \times 1000 \text{mm} = 1.000.000.000 \text{mm}^3 $$
Anche in questo caso si può usare la notazione esponenziale su base dieci
$$ 1 \text{m}^3 = 10^3 \text{mm} \times 10^3 \text{mm} \times 10^3 \text{mm} = (10^3)^3 \text{mm}^3 = 10^9 \text{mm}^3 $$
Questa unità è utile per misurare volumi estremamente piccoli, come quelli di piccole gocce o minuscole cavità.
Allo stesso modo, puoi passare ai multipli del metro cubo quando si tratta di volumi molto grandi:
4] Da metri cubi (m³) a ettometri cubi (hm³)
Un ettometro cubo (hm³) corrisponde a 1.000.000 metri cubi:
$$ 1 \text{hm}^3 = 100 \text{m} \times 100 \text{m} \times 100 \text{m} = 1.000.000 \text{m}^3 $$
In notazione esponenziale si scrive:
$$ 1 \text{hm}^3 = 10^2 \text{m} \times 10^2 \text{m} \times 10^2 \text{m} = (10^2)^3 \text{m}^3 = 10^6 \text{m}^3 $$
Questa unità è spesso usata per misurare il volume di bacini idrici o grandi serbatoi.
5] Da metri cubi (m³) a chilometri cubi (km³)
Un chilometro cubo (km³) equivale a 1.000.000.000 di metri cubi:
$$ 1 \text{km}^3 = 1000 \text{m} \times 1000 \text{m} \times 1000 \text{m} = 1.000.000.000 \text{m}^3 $$
In notazione esponenziale
$$ 1 \text{km}^3 = 10^3 \text{m} \times 10^3 \text{m} \times 10^3 \text{m} = (10^3)^3 \text{m}^3 = 10^9 \text{m}^3 $$
È un'unità utilizzata per misurare volumi naturali enormi, come quelli dei laghi, delle montagne o delle nuvole atmosferiche.
Esempio pratico: quanti dm3 ci sono in 7 hm3? Vediamo come convertire da un multiplo a un sottomultiplo (o viceversa) dell'unità di misura del volume utilizzando una metodologia che si basa sulle potenze dei prefissi, che funziona benissimo per le conversioni tridimensionali come quelle di volume. Parti dall'equivalenza: $$ 7 \ \text{hm}^3 = x \ \text{dm}^3 $$ Sostituisci il prefisso $ h $ con \(10^2\) poiché 1 hm = \(10^2\) m e il prefisso $ d $ con \(10^{-1}\) poiché 1 dm = \(10^{-1}\) m, ricordando di elevare tutto al cubo poiché stiamo parlando di volume ovvero di una grandezza tridimensionale: $$ 7 \cdot (10^2 \text{m})^3 = x \cdot (10^{-1} \text{m})^3 $$ Calcola le potenze $$ 7 \cdot 10^6 \text{m}^3 = x \cdot 10^{-3} \text{m}^3 $$ Isola \(x\) $$ x = 7 \cdot 10^9 $$ Quindi, 7 hm³ = 7.000.000.000 dm³