Le grandezze inversamente proporzionali
Due grandezze sono inversamente proporzionali se il loro prodotto è sempre uguale a una costante \( k \). Questo si esprime matematicamente come: $$ x \cdot y = k $$ o, equivalentemente, isolando \( y \): $$ y = \frac{k}{x} $$
Dove \( k \) è il coefficiente di proporzionalità inversa, una costante che caratterizza la relazione tra le due grandezze.
Questo significa che, se \( x \) aumenta, \( y \) diminuisce in modo tale che il prodotto rimanga invariato, e viceversa.
Ma cosa significa tutto questo in termini pratici? Facciamo un esempio pratico.
Esempio concreto
Immagina che una piazza debba essere pulita dopo una festa di paese.
Se il lavoro viene svolto da una sola persona, questa impiegherà 100 ore per pulire la piazza.
Se più persone collaborano, il tempo richiesto diminuisce in modo proporzionale al numero di lavoratori, seguendo la formula:
$$ t = \frac{100}{n} $$
Dove \( t \) è il tempo impiegato per completare il lavoro (in ore), \( n \) è il numero di lavoratori, \( 100 \) è il totale delle ore richieste per il lavoro (costante).
Questa tabella mostra il tempo necessario per completare il lavoro in base al numero di lavoratori.
| Numero di lavoratori (n) | Tempo per completare il lavoro (t) [ore] | Prodotto n * t (ore totali) |
|---|---|---|
| 1 | 100.0 | 100.0 |
| 2 | 50.0 | 100.0 |
| 4 | 25.0 | 100.0 |
| 5 | 20.0 | 100.0 |
| 10 | 10.0 | 100.0 |
| 20 | 5.0 | 100.0 |
La tabella mostra come il tempo per completare un lavoro di 100 ore diminuisce al crescere del numero di lavoratori, mantenendo costante il prodotto \( n \cdot t = 100 \).
Ad esempio, impiegando due lavoratori il tempo per pulire la piazza scende a 50 ore. Con quattro lavoratori, il tempo scende ulteriormente a 25 ore. Con venti lavoratori solo 5 ore, e via dicendo.
Se rappresentiamo graficamente questa relazione con \( n \) sull’asse orizzontale e \( t \) sull’asse verticale, otterremo una curva iperbolica.
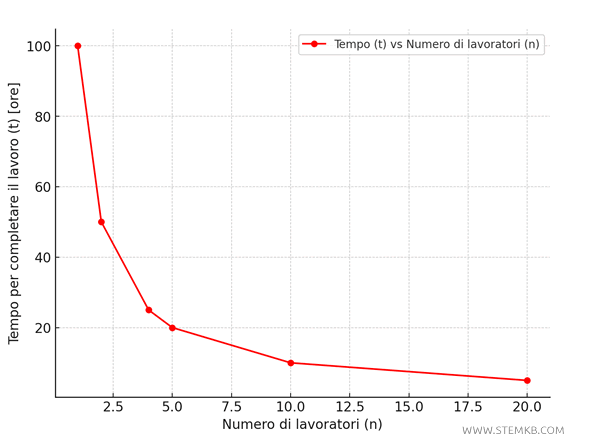
Questo tipo di curva ha una caratteristica forma "a braccia aperte" e riflette l'idea che, man mano che una grandezza aumenta, l'altra diminuisce, senza mai raggiungere un valore nullo.
Quindi, le grandezze inversamente proporzionali rappresentano una relazione per descrivere fenomeni in cui due quantità si compensano reciprocamente.
In natura molti fenomeni tendono a bilanciarsi seguendo questo tipo di relazione.
Ad esempio, un esempio classico di proporzionalità inversa è la legge di Boyle, che stabilisce che il prodotto tra pressione (\(P\)) e volume (\(V\)) di un gas a temperatura costante è sempre uguale a una costante: $$ P \cdot V = k $$ Quando il volume di un gas diminuisce, la pressione aumenta proporzionalmente, e viceversa. In altre parole, se comprimiamo un gas riducendo il suo volume, la pressione aumenta; al contrario, se lo lasciamo espandere, la pressione diminuisce.