Misure in accordo e in disaccordo
Le misure in accordo sono quelle misure che sono allineate o compatibili tra loro, generalmente entro un margine di errore accettabile o una certa tolleranza. Viceversa, le misure in disaccordo sono misure che differiscono in modo significativo, superando il margine di errore accettabile.
Nel mondo della statistica e delle scienze delle misurazioni, ottenere "misure in accordo" è fondamentale per garantire la qualità e la precisione dei dati.
Queste misure, che rimangono entro un margine di errore accettabile, rappresentano il segnale che i risultati raccolti sono coerenti, affidabili e possono essere considerati validi per ulteriori analisi e decisioni.
Al contrario, quando ci troviamo di fronte a "misure in disaccordo", emergono dubbi sulla validità dei dati, spesso richiedendo ulteriori verifiche e possibili correzioni.
Un esempio
Consideriamo due gruppi sperimentali che hanno misurato la massa \( m \) di un oggetto e hanno ottenuto i seguenti risultati:
- Esperimento 1: \( m = (5,12 \pm 0,05) \, \text{g}\)
- Esperimento 2: \( m = (5,08 \pm 0,04) \, \text{g} \)
Se guardassimo solo i valori centrali (5,12 g e 5,08 g), potremmo concludere che le misure siano discordanti, poiché i valori medi differiscono.
Tuttavia, per valutare correttamente la compatibilità delle misure, dobbiamo considerare gli intervalli di incertezza associati a ciascuna misura.
Nel primo esperimento, la massa è stata misurata come \( 5,12 \, \text{g} \) con un'incertezza di \( \pm 0,05 \, \text{g} \). Ciò significa che l'intervallo di possibile valore della massa è:
$$ 5,12 - 0,05 = 5,07 \, \text{g} \quad \text{e} \quad 5,12 + 0,05 = 5,17 \, \text{g} $$
Quindi l'intervallo è \( [5,07 \, \text{g}, 5,17 \, \text{g}] \).
Nel secondo esperimento, la massa è stata trovata pari a \( 5,08 \, \text{g} \) con un'incertezza di \( \pm 0,04 \, \text{g} \).
L'intervallo della massa risulta quindi:
$$ 5,08 - 0,04 = 5,04 \, \text{g} \quad \text{e} \quad 5,08 + 0,04 = 5,12 \, \text{g} $$
In questo caso, l'intervallo è \( [5,04 \, \text{g}, 5,12 \, \text{g}] \).
Confrontando i due intervalli:
- Primo esperimento: \( [5,07 \, \text{g}, 5,17 \, \text{g}] \)
- Secondo esperimento: \( [5,04 \, \text{g}, 5,12 \, \text{g}] \)
Notiamo che gli intervalli si sovrappongono nell'intervallo comune \( [5,07 \, \text{g}, 5,12 \, \text{g}] \).
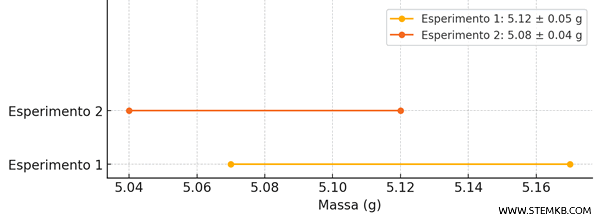
Poiché esiste un’intersezione tra i due intervalli di incertezza, possiamo concludere che le misure sono compatibili o in accordo entro i limiti dell'errore sperimentale.
Ciò significa che il valore reale della massa potrebbe trovarsi simultaneamente in entrambi gli intervalli di incertezza, e quindi non ci sono discrepanze significative tra i risultati dei due esperimenti.
Le misure in accordo, dunque, non sono solo una conferma della qualità dei dati, ma servono anche come strumento per rafforzare la fiducia negli strumenti e nelle metodologie utilizzate.
Quando i risultati di differenti misurazioni coincidono, ci troviamo in una posizione più sicura per affermare che il fenomeno osservato è stato rappresentato con accuratezza.
Viceversa, se le letture differiscono senza sovrapporsi, superando la soglia di tolleranza, avremo delle "misure in disaccordo". Ad esempio, supponiamo di fare un terzo esperimento che restituisce un risultato $ 5.3 \pm 0.03 \ g $ non sovrapposto nemmeno parzialmente ai precedenti. In questo caso avremo delle misure in disaccordo tra loro.
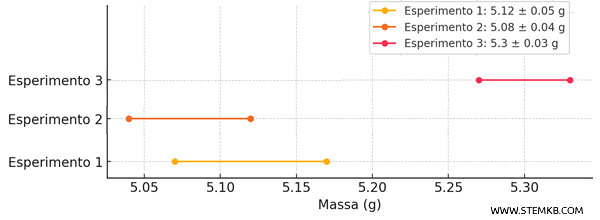
Questo potrebbe indicare un problema di calibrazione in uno dei termometri, o magari una metodologia di misurazione che influisce sui risultati. In alcuni casi, la causa può essere un errore umano o, ancora, una condizione ambientale che ha influenzato il processo di misura.
Cosa fare se le misure sono in disaccordo?
Quando si osservano misure in disaccordo, è necessario un lavoro di diagnosi: si può ricorrere a test di controllo, confrontare gli strumenti con standard noti, o approfondire le caratteristiche del metodo utilizzato.
Ad esempio, se un test produce risultati inconsistenti rispetto a quelli di un test considerato più accurato, è importante verificare sia il test che lo strumento, per comprendere se l’anomalia sia un errore strumentale o una reale caratteristica della patologia in esame.
In conclusione, la distinzione tra misure in accordo e in disaccordo non è solo un fattore tecnico, ma è il cuore di un approccio scientifico rigoroso che mira a costruire dati solidi e affidabili.
Le misure in accordo ci danno la sicurezza per avanzare con analisi più complesse, mentre le misure in disaccordo ci spingono a riflettere e investigare sul processo di misura dei fenomeni osservati.