Le cifre significative in fisica

Le cifre significative sono tutte le cifre di un numero che contribuiscono a descrivere con precisione il valore di una grandezza misurata. Includono tutte le cifre certe e la prima cifra incerta.

In pratica, rappresentano il grado di accuratezza e di precisione con cui una misura è stata effettuata.

Quando misuri una grandezza fisica, come il volume di un liquido, la temperatura o la lunghezza di un oggetto, utilizzi uno strumento che ha una sua precisione intrinseca.

Le cifre significative comprendono tutte quelle che lo strumento di misura riesce a determinare, in base alla sua sensibilità.

In altre parole, il numero di cifre significative dipende dalla precisione dello strumento: più sensibile è lo strumento, più cifre significative si possono riportare.

Un esempio

Immagina di misurare la lunghezza di una matita utilizzando un righello che ha divisioni di 0,1 cm.

Ottieni un valore di 15,2 cm.

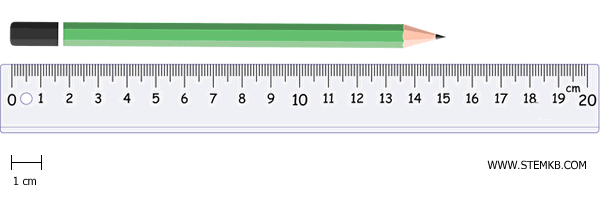
esempio di misura

In questo caso, siamo certi delle cifre "1" e "5" (la parte intera), mentre la cifra decimale "2" è soggetta a un certo grado di incertezza, poiché dipende dalla precisione dello strumento, ovvero dalla minima suddivisione indicata.

In questo esempio, la misura 15,2 cm ha tre cifre significative: le prime due sono cifre certe (o cifre esatte), mentre la terza è incerta, ma significativa.

Tra queste cifre significative, le cifre certe sono quelle che rimangono costanti entro l'intervallo di incertezza della misura. In pratica, le cifre certe non cambiano in base all’errore associato alla misura, quindi sono quelle su cui possiamo fare affidamento con maggiore sicurezza. In questo caso la misura della matita è 15,2 cm utilizzando un righello con i millimetri, l'intervallo di incertezza dovuto al righello sarà $ \pm 0,5 \ mm $ ossia $ \pm 0,05 \ cm $: $$ 15,2 \, \text{cm} \pm 0,05 \, \text{cm} $$ Quindi, l'intervallo entro cui si trova la lunghezza reale della matita sarà compreso tra 15,15 cm e 15,25 cm. Le uniche cifre che non cambiano sono 1 e 5, quindi 1 e 5 sono le cifre certe della misura.

Perché le cifre significative sono importanti?

Le cifre significative ti indicano non solo il valore numerico di una misura, ma anche la precisione con cui tale valore è stato determinato.

È essenziale tenerle in considerazione quando si eseguono calcoli con i valori misurati, poiché ogni cifra aggiuntiva porta con sé un'interpretazione differente della precisione della misura stessa.

Ad esempio, se scrivi 15,20 cm invece di 15,2 cm, stai dicendo che la misura è stata effettuata con una precisione di 0,01 cm, e che quindi la cifra "0" dopo il "2" è anch'essa significativa. In questo caso, le cifre significative diventano quattro. Pertanto, la scrittura 15,20 cm è diversa da 15,2 cm perché non fornisce la stessa informazione. La prima misura è molto più precisa.

Come si contano le cifre significative?

In generale valgono le seguenti regole:

Numeri diversi da zero sono sempre significativi.
Ad esempio, in 1234, tutte e quattro le cifre sono significative.
Zeri tra due cifre significative (zeri interni) sono anch'essi significativi.
Ad esempio, in 102, i tre numeri sono significativi.
Zeri a sinistra di un numero non sono significativi, poiché servono solo come posizionamento decimale.
Ad esempio, in 0,0056, le cifre significative sono solo 5 e 6.
Zeri finali di un numero che contiene una virgola decimale sono significativi.
Ad esempio, 45,00 ha quattro cifre significative perché gli zeri finali indicano la precisione della misurazione.
Zeri finali di un numero senza virgola decimale possono o non possono essere significativi.
Ad esempio, in 1500, il numero di cifre significative dipende dal contesto o dalla notazione utilizzata.

Qualche esempio pratico

Per comprendere meglio il conteggio delle cifre significative, consideriamo alcuni esempi:

0,0045 ha due cifre significative: i primi tre zeri non sono significativi perché servono solo a posizionare la cifra "4" dopo la virgola.
8,300 ha quattro cifre significative: lo zero alla fine è significativo perché indica la precisione della misura.
0,0560 ha tre cifre significative: i primi due zeri non contano, ma lo zero alla fine sì, perché comunica la precisione della misura.

In alcuni casi, però, gli zeri finali di un numero intero possono creare ambiguità.

Ad esempio, un valore come 1400 m potrebbe avere due, tre o quattro cifre significative, a seconda se consideri gli zeri come parte della precisione della misura o solo come posizioni decimali.

Per evitare confusione, si utilizza la notazione scientifica.

Questo metodo ti permette di indicare chiaramente quante cifre significative ha un numero. Ad esempio:

Se scrivi 1,4 × 10³ m, stai dicendo che il valore ha due cifre significative. Quindi, il margine di incertezza e di 0,1 m.
Se scrivi 1,40 × 10³ m stai comunicando che il numero ha tre cifre significative. In questo caso, il margine di incertezza e di 0,01 m.
Se scrivi 1,400 × 10³ m stai affermando che il numero ha ben quattro cifre significative. In quest'ultimo caso, il margine di incertezza e di 0,001 m.

Come puoi notare il numero è sempre lo stesso... ma il margine di incertezza sulla precisione del numero è molto diversa.

Le operazioni con le cifre significative

Quando svolgi le operazioni matematiche tra misure di grandezze fisiche, ricorda di rispettare le regole delle cifre significative. Queste regole garantiscono che il risultato dell’operazione non venga presentato con una precisione maggiore di quella delle grandezze coinvolte.

Arrotondamento di un numero
Per arrotondare un numero, si segue una regola base molto semplice:
- Se la prima cifra da eliminare è minore di 5, la cifra precedente resta invariata.
  Ad esempio, l'arrotondamento di $4,372 $ da 4 cifre significative a 3 cifre significative è $ 4,37 $. Poiché l'ultima cifra significativa ($4,37\color{red}2 $) è minore di 5, la precedente cifra ($4,3\color{red}72 $) resta invariata ($4,3\color{red}7 $) .
- Se la prima cifra da eliminare è 5 o superiore, la cifra precedente aumenta di un’unità.
  Ad esempio, l'arrotondamento di $4,376 $ da 4 cifre significative a 3 cifre significative è $ 4,38 $. In questo caso l'ultima cifra significativa ( $4,37\color{red}6 $) è maggiore-uguale di 5, quindi la precedente cifra ( $4,3\color{red}76 $) aumenta di un'unità (7+1=8) e il numero arrotondato è ( $4,3\color{red}8 $)
Moltiplicazione o divisione di due grandezze
Nel caso di una moltiplicazione o divisione tra due grandezze, il risultato deve avere lo stesso numero di cifre significative della grandezza che ne ha di meno. Questo significa che la precisione del risultato è limitata dalla misura meno precisa.
Ad esempio, svolgi questa moltiplicazione $$ (4,376 \, m) \cdot (1,4 \, m) = 6,1264 \, m^2 $$ Poiché la grandezza meno precisa ha 2 cifre significative (1,4 m), anche il risultato devi arrotondarlo a 2 cifre significative. $$ (4,376 \, m) \cdot (1,4 \, m)= 6,1264 \, m^2 \approx 6,1 \, m^2 $$
Moltiplicazione o divisione di una grandezza per un numero
Quando una grandezza viene moltiplicata o divisa per un numero puro, il risultato deve mantenere lo stesso numero di cifre significative della grandezza. Questo perché la precisione del numero puro non influisce sulla precisione complessiva dell'operazione, è solo la grandezza fisica stessa a determinare quante cifre significative devono apparire nel risultato.
Ad esempio, moltiplica $ 5,678 \ m $ per $ 3 $ $$ (5,678 \, m) \cdot 3 = 17,034 \, m $$ Poiché 5,678 ha 4 cifre significative, anche il risultato ( 17,034 m ) devi arrotondarlo a 4 cifre significative ( 17,03 m ). $$ (5,678 \, m) \cdot 3 = 17,034 \, m \approx 17,03 \, m $$
Addizione o sottrazione di due grandezze
Per l’addizione o sottrazione, il risultato deve avere lo stesso numero di cifre decimali della grandezza con il minor numero di decimali. In questo caso, devi arrotondare gli addendi a quello con il minore numero di cifre decimali. In alternativa, puoi sommare i termini originale e poi arrotondare il risultato.

Ad esempio, somma $ 12,3 \ s $ e $ 4.678 \ s $ $$ 12,3 \, s + 4,678 \, s $$ In questo caso, 12,3 s ha una sola cifra decimale, quindi devi arrotondare anche l'altro addendo a una sola cifra decimale ( $ 4,678 \ s \rightarrow 4,7 \ s $ ) . $$ 12,3 \, s + 4,678 \, s = 12,3 \, s + 4,7 \, s $$ Dopo aver portato tutti gli addendi allo stesso numero di cifre decimali, puoi procedere con la somma. In questo caso il risultato è $ 17,0 \ s $. $$ 12,3 \, s + 4,678 \, s = 12,3 \, s + 4,7 \, s = 17,0 \, s $$

Seguendo queste semplici regole, eviti di attribuire al risultato finale una precisione irrealistica e mantieni il rigore scientifico necessario nelle misure fisiche. Questo approccio permette di interpretare i dati in maniera chiara e affidabile.

In conclusione, le cifre significative non sono solo un dettaglio tecnico o estetico, sono essenziali per esprimere con chiarezza e precisione i risultati delle misurazioni scientifica.

Ogni cifra in più o in meno può cambiare l’interpretazione della misura e, di conseguenza, può influenzare sia i calcoli che le decisioni che si prendono.

Le cifre significative sono fondamentali in chimica, fisica, e in molte altre discipline scientifiche per comunicare con precisione i risultati delle misurazioni, evitando ambiguità e indicare la qualità dello strumento di misura utilizzato.