La rappresentazione dei dati tramite i grafici
Quando si cerca di comprendere le relazioni tra due grandezze in un contesto scientifico o pratico, i grafici cartesiani rappresentano uno strumento essenziale.
Questi diagrammi, ideati nel 1637 dal filosofo e matematico francese René Descartes (o Cartesio), consentono di visualizzare dati e relazioni in modo chiaro e intuitivo. A partire da un’intuizione del XVII secolo, oggi sono uno strumento indispensabile per trasformare dati grezzi in informazioni significative.
Un grafico cartesiano si basa su due assi perpendicolari:
- Asse delle ascisse (orizzontale), generalmente usato per rappresentare la grandezza indipendente.
- Asse delle ordinate (verticale), destinato alla grandezza dipendente.
Ogni punto sul grafico corrisponde a una coppia di valori, uno per ciascun asse.
Un esempio pratico
In questo esempio studiamo la relazione tra il tempo e la distanza percorsa da un ciclista.
Scegliamo di misurare il tempo sull’asse delle ascisse e la distanza sull’asse delle ordinate.
Immaginiamo di aver raccolto i dati di un ciclista che parte da fermo. La tabella seguente riporta i valori registrati ogni quarto d’ora:
| Tempo \( t \) (min) | Distanza \( d \) (km) |
|---|---|
| 0 | 0 |
| 15 | 4 |
| 30 | 8 |
| 45 | 12 |
| 60 | 16 |
| 75 | 20 |
| 90 | 24 |
Questi dati possono essere rappresentati su un grafico cartesiano:
- Sull’asse delle ascisse \( t \), fissiamo un’unità corrispondente a 15 minuti.
- Sull’asse delle ordinate \( d \), scegliamo un’unità che renda facile distinguere le distanze, ad esempio 4 km.
I punti risultanti (\( t, d \)) formano una linea retta, indicando una relazione lineare tra il tempo e la distanza. Questo significa che il ciclista si muove a velocità costante: per ogni incremento di 15 minuti, percorre 4 km.
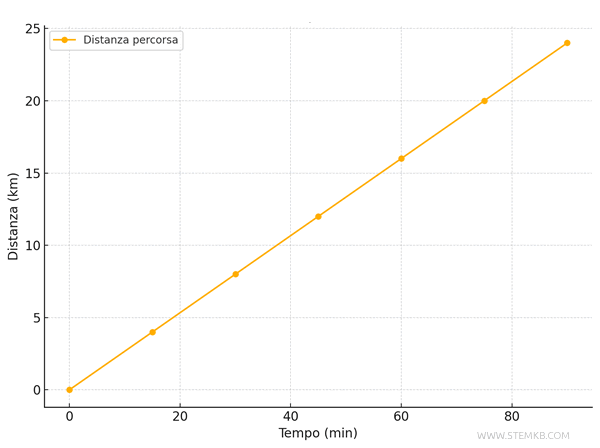
A colpo d'occhio si nota subito la costanza della velocità, essendo il grafico una linea, e la pendenza della retta rappresenta la velocità.
In questo caso il ciclista percorre 4 km ogni 15 minuti, quindi la sua velocità è pari a 16 km/h.
Esempio 2
Vediamo cosa accade quando i dati rilevati sono diversi.
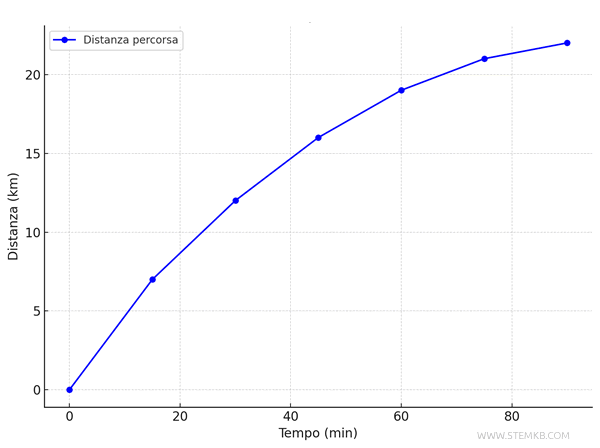
Un secondo ciclista percorre la stessa strada.
| Tempo \( t \) (min) | Distanza \( d \) (km) |
|---|---|
| 0 | 0 |
| 15 | 7 |
| 30 | 12 |
| 45 | 16 |
| 60 | 19 |
| 75 | 21 |
| 90 | 22 |
In questo caso il grafico mostra un andamento differente.
Dalla linea curva possiamo subito notare che la velocità non è costante. Inizialmente il ciclista va più veloce, poi riduce progressivamente la sua velocità, forse a causa della stanchezza.
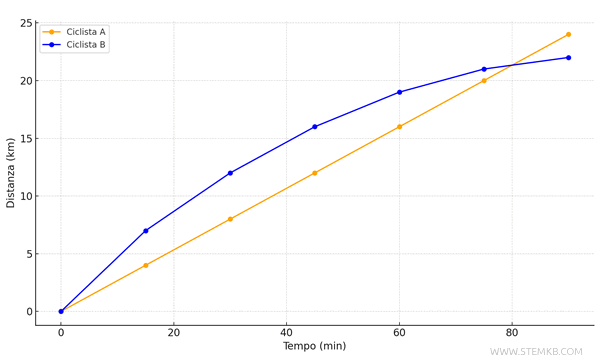
Confrontando i due grafici nello stesso diagramma si vede chiaramente che il primo ciclista, quello che mantiene una velocità costante, percorre una maggiore distanza e a un certo punto supera il secondo ciclista.
Quali sono i vantaggi della rappresentazione grafica?
Il grafico cartesiano offre immediatamente informazioni che altrimenti sarebbero meno evidenti osservando solo i numeri.
In conclusione, i grafici trasformano i numeri in strumenti visivi di comunicazione, rendendo i dati più comprensibili.