L'area: grandezza derivata per misurare le superfici

L’area è una grandezza della geometria e della fisica che ti permette di quantificare l’estensione di una superficie. L’area di una superficie è data dal prodotto di due lunghezze. $$ \text{Area} = [L] \cdot [L] $$

L'area è una grandezza fisica derivata perché si calcola a partire da una grandezza fondamentale, ovvero la lunghezza [L].

Ad esempio, l’area di un rettangolo si calcola moltiplicando la lunghezza della base per l’altezza:

$$ \text{Area del rettangolo} = \text{base} \times \text{altezza} $$

Misurare l’area ti aiuta a capire quanto spazio occupa una figura piana come un rettangolo, un quadrato o qualsiasi altra forma geometrica.

L'unità di misura dell'area

L’unità di misura standard per l’area è il metro quadrato ($ m^2 $), che rappresenta l’area di un quadrato i cui lati misurano esattamente 1 metro ciascuno.

$$ 1 \, \text{m}^2 = (1 \, \text{m}) \times (1 \, \text{m}) $$

Quando misuri l’area di una superficie in metri quadrati, stai essenzialmente determinando quanti quadrati di lato 1 metro possono essere disposti su quella superficie.

Un esempio pratico

Ad esempio, se consideri un rettangolo di 10 metri di base e 5 metri di altezza.

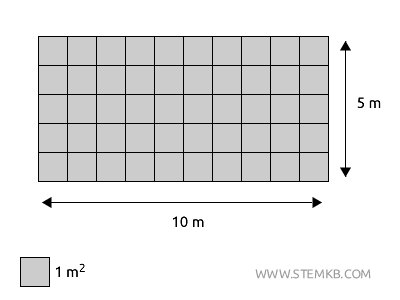
L’area del rettangolo è il prodotto della lunghezza della base (10 m) per la lunghezza dell'altezza (5 m)

$$ \text{Area} = (10 \, \text{m}) \times (5 \, \text{m}) = 50 \, \text{m}^2 $$

Nota che non si moltiplicano solo i numeri $ 10 \times 5 = 50 $, ma anche le unità di misura \( \text{m} \times \text{m} = \text{m}^2 \).

In questo esempio, nel rettangolo ci sono 50 quadrati di lato 1 metro.

Questo riflette il fatto che l'area è una grandezza che misura quanta superficie viene coperta, e l’uso di m² indica che stai considerando il prodotto di due lunghezze lineari, cioè una superficie.

I multipli e i sottomultipli del metro quadrato

Le unità di misura dell’area puoi esprimerle anche in termini di multipli e sottomultipli del metro quadrato, come il centimetro quadrato ( $ cm^2 $), il millimetro quadrato ( $ mm^2 $) e il chilometro quadrato ( $ km^2 $ ).

È importante però conoscere come si convertono queste unità per evitare errori.

Ricorda che l'area è il prodotto di due lunghezze. Quindi, ogni volta che cambi l’unità di misura, il fattore di conversione viene elevato al quadrato.

Vediamo qualche esempio:

• Passare dai metri quadrati ($ m^2 $) ai decimetri quadrati ($ dm^2 $) implica moltiplicare per $ (10)^2 $, ovvero 100.
• Passare dai metri quadrati ($ m^2 $) ai centimetri quadrati ($ cm^2 $) implica moltiplicare per $ (10^2)^2 $, ovvero 10.000.
• Passare dai metri quadrati ($ m^2 $) ai millimetri quadrati ($ mm^2 $) implica moltiplicare per $ (10^3)^2 $ ovvero 1.000.000.

Quindi, è fondamentale applicare correttamente il fattore di conversione per evitare errori significativi.

Un centimetro quadrato è l’area di un quadrato con lato di 1 cm. Convertito in metri, 1 cm equivale a \(10^{-2}\) metri. Pertanto:

$$ 1 \, \text{cm}^2 = (1 \, \text{cm}) \times (1 \, \text{cm}) = (10^{-2} \, \text{m}) \times (10^{-2} \, \text{m}) = 10^{-4} \, \text{m}^2 = 0,0001 \, \text{m}^2 $$

Un millimetro equivale a \(10^{-3}\) metri, quindi un millimetro quadrato equivale a \( 10^{-6} \) metri quadrati.

$$ 1 \, \text{mm}^2 = (1 \, \text{mm}) \times (1 \, \text{mm}) = (10^{-3} \, \text{m}) \times (10^{-3} \, \text{m}) = 10^{-6} \, \text{m}^2 = 0,000001 \, \text{m}^2 $$

Un chilometro equivale a \(10^3\) metri, quindi un chilometro quadrato equivale a \( 10^{6} \) metri quadrati.

$$ 1 \, \text{km}^2 = (1 \, \text{km}) \times (1 \, \text{km}) = (10^3 \, \text{m}) \times (10^3 \, \text{m}) = 10^6 \, \text{m}^2 = 1.000.000 \, \text{m}^2 $$

E via dicendo. Pertanto, fai molta attenzione a non sbagliare quando converti il metro quadrato.