Grandezze linearmente dipendenti
In fisica, molte delle relazioni che descrivono fenomeni naturali si possono esprimere in termini matematici. Tra queste, un caso particolarmente significativo è rappresentato dalle grandezze linearmente dipendenti, che si collegano tramite una relazione semplice ma potente:
\[ y = kx + y_0 \]
Questa equazione lineare racchiude una connessione diretta e prevedibile tra due grandezze fisiche.
E' uno strumento essenziale per analizzare e comprendere sistemi di ogni tipo, dal moto rettilineo uniforme al funzionamento dei circuiti elettrici.
La relazione lineare
L'equazione \( y = kx + y_0 \) descrive una dipendenza lineare tra due variabili: \( x \) e \( y \). Ecco cosa rappresentano i suoi elementi:
- \( k \) è il coefficiente angolare o pendenza della retta. Indica come varia \( y \) quando \( x \) cambia di una certa quantità. Ad esempio, in una relazione diretta proporzionale, \( k \) rappresenta il tasso di variazione costante.
- \( y_0 \) è il termine noto o l'intercetta sull'asse \( y \). Determina il valore di \( y \) quando \( x = 0 \). Questa componente sposta la retta verticalmente nel piano cartesiano.
- \( x \) e \( y \) sono le grandezze fisiche che stiamo mettendo in relazione. Spesso, \( x \) è la grandezza indipendente, mentre \( y \) è quella dipendente.
Un esempio pratico è il moto rettilineo uniforme, in cui la posizione di un corpo (\( s \)) è una funzione lineare del tempo (\( t \)):
\[ s = vt + s_0 \]
Qui, \( v \) è la velocità costante, \( t \) il tempo e \( s_0 \) la posizione iniziale.
Un esempio concreto
Un'applicazione iconica della dipendenza lineare è la Legge di Ohm nei circuiti elettrici.
Questa legge afferma che la tensione (\( V \)) su un conduttore è direttamente proporzionale alla corrente (\( I \)) che lo attraversa, con la resistenza (\( R \)) come costante di proporzionalità:
$$ V = RI $$
In questo caso, il coefficiente angolare è \( k = R \) e il termine noto è nullo \( y_0 = 0 \). Pertanto, si tratta di una proporzionalità diretta senza termine noto.
L'importanza di questa relazione risiede nella sua semplicità: conoscendo due delle tre variabili, è possibile calcolare la terza.
Altri esempi pratici. In fisica possiamo trovare molti altri esempi di dipendenza lineare tra grandezze. Ad esempio, nella legge di Hooke, la forza (\( F \)) esercitata su una molla è proporzionale alla sua estensione (\( x \)): $$ F = kx $$ E' solo un altro esempio tra i tanti possibili.
Esempio 2
Consideriamo la relazione lineare \( y = 2x + 3 \), dove \( k = 2 \) è la pendenza e \( y_0 = 3 \) è il termine noto.
$$ y = 2x+ 3 $$
Calcoliamo i valori di \( y \) per diversi valori di \( x \), ad esempio da 0 a 10.
Ecco una tabella che mostra i valori di \( x \) e i corrispondenti valori di \( y \) calcolati in base alla relazione lineare \( y = 2x + 3 \).
| x | y |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
| 6 | 15 |
| 7 | 17 |
| 8 | 19 |
| 9 | 21 |
| 10 | 23 |
Ogni incremento di \( x \) di una unità produce un incremento costante di \( y \) pari a 2 (il coefficiente angolare \( k \)).
Nel grafico, i punti risultano perfettamente allineati lungo una retta.
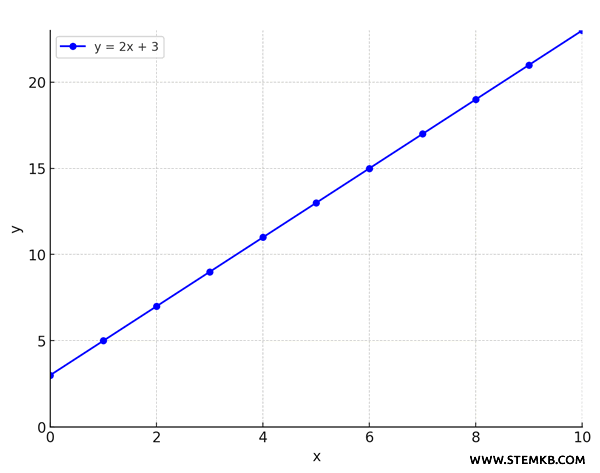
Questa caratteristica conferma visivamente la natura lineare della relazione.
Vantaggi della linearità
Le relazioni lineari sono così fondamentali perché rendono le equazioni facilmente risolvibili e i dati prevedibili.
Se conosciamo \( k \) e \( y_0 \), possiamo calcolare il valore di \( y \) per qualsiasi \( x \).
Questa semplicità di consente di modellare fenomeni complessi e creare previsioni accurate.
Per questa ragione, le grandezze linearmente dipendenti sono un pilastro della fisica e della matematica applicata.
La linearità rappresenta spesso il punto di partenza per analisi più complesse, ci fornisce una base solida su cui costruire modelli avanzati. Osservando il mondo attraverso la lente di queste relazioni, possiamo vedere ordine e regolarità anche nei fenomeni più apparentemente caotici.