Il moto rettilineo uniforme
Il moto rettilineo uniforme si verifica quando un oggetto si muove lungo una linea retta a velocità costante. Non ci sono forze che cambiano la velocità dell'oggetto.
Le principali caratteristiche di questo moto sono:
- Il moto avviene in linea retta.
- La velocità \( v \) è costante.
Legge del moto rettilineo uniforme
La formula per descrivere il moto rettilineo uniforme è:
$$ s = s_0 + vt $$
Dove:
- \( t \) è qualsiasi istante di tempo ossia il tempo trascorso.
- \( s \) è la posizione dell'oggetto a un tempo \( t \) qualsiasi.
- \( s_0 \) è la posizione iniziale dell'oggetto al tempo \( t = 0 \).
- \( v \) è la velocità costante.
Grafico spazio-tempo
Immagina un grafico dove l'asse verticale rappresenta la posizione \( s \) e l'asse orizzontale rappresenta il tempo \( t \).
Per il moto rettilineo uniforme il grafico è una linea retta.
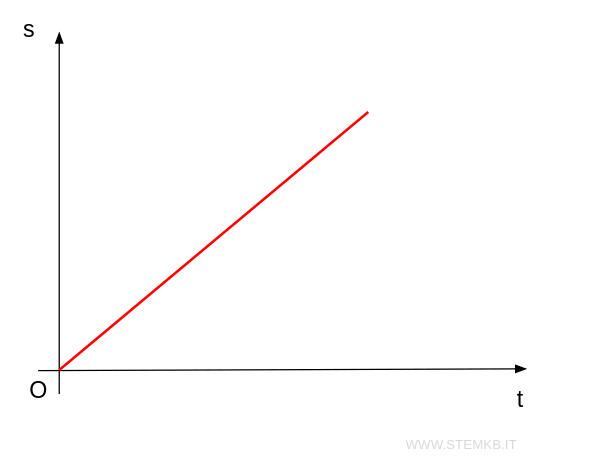
La linea retta interseca l'asse delle posizioni al punto \( s_0 \) quando il tempo \( t \) è 0 ovvero nell'istante iniziale del moto.
In altre parole, se parti da una posizione iniziale \( s_0 \), la posizione finale \( s \) dopo un certo tempo \( t \) sarà \( s_0 + vt \).
Se la posizione iniziale è \( s_0 = 0 \) (cioè parti dall'origine), la formula si semplifica a: $$ s = vt $$
Un esempio pratico
Certo, facciamo un esempio pratico per chiarire il concetto di moto rettilineo uniforme.
Immagina di avere un'auto che si muove lungo una strada rettilinea a una velocità costante di 60 km/h.
L'autmobile si muove a velocità costante \( v = 60 km/h \) per un tempo \( t = 2 \ ore \):
Partiamo dal presupposto che iniziamo a misurare la posizione dell'auto a partire da un punto specifico di partenza che chiamiamo \( s_0 = 0 \ km \).
Utilizziamo la formula del moto rettilineo uniforme:
$$ s = s_0 + vt $$
I dati del problema sono
- \( s_0 = 0 \) km (posizione iniziale)
- \( v = 60 \) km/h (velocità costante)
- \( t = 2 \) ore (tempo trascorso)
Ora, sostituiamo questi valori nella formula:
$$ s = 0 + 60 \times 2 $$
$$ s = 0 + 120 $$
$$ s = 120 $$
Dopo 2 ore, l'auto si troverà a 120 km dal punto di partenza.
Adesso rappresentiamo questo movimento su un grafico spazio-tempo:
L'asse orizzontale (x) rappresenta il tempo \( t \) in ore mentre l'asse verticale (y) rappresenta la posizione \( s \) in chilometri.
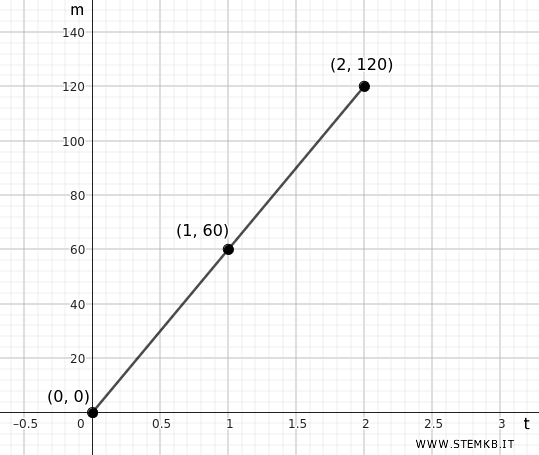
Per ogni ora che passa, l'auto percorre 60 km. Quindi, il grafico sarà una linea retta che parte dall'origine (0,0) e sale costantemente verso destra con una pendenza che rappresenta la velocità costante di 60 km/h.
Ecco la tabella che mostra la posizione dell'auto a diversi istanti di tempo:
\[
\begin{array}{|c|c|}
\hline
\text{Tempo (ore)} & \text{Posizione (km)} \\
\hline
0 & 0 \\
1 & 60 \\
2 & 120 \\
\hline
\end{array}
\]
Questa tabella mostra come la posizione dell'auto cambia linearmente con il tempo, seguendo la legge del moto rettilineo uniforme \( s = s_0 + vt \).
Quindi, il punto (1,60) sul grafico rappresenta la posizione dell'auto dopo 1 ora mentre il punto \( (2, 120) \) la posizione dell'auto dopo 2 ore.
Spero che questo esempio ti aiuti a comprendere meglio il concetto di moto rettilineo uniforme.