L'errore assoluto in una misura
Cos’è l’errore assoluto?
L’errore assoluto $ e_x $ rappresenta l’incertezza o l’imprecisione di una misura rispetto a un valore medio $ \bar{x} $ o a un insieme di misurazioni. $$ x = \bar{x} \pm e_x $$
È un modo per esprimere quanto una misura potrebbe differire dal valore reale a causa delle inevitabili variazioni nella misurazione.
Come si calcola l'errore assoluto?
Per stimare l’incertezza di una misura basata su una serie di valori osservati, uno dei metodi più semplici ed efficaci è il calcolo dell’errore assoluto attraverso la semidispersione.
La semidispersione è una stima dell’errore assoluto che si ottiene dividendo per due la differenza tra il valore massimo e il valore minimo osservati:
$$ e_{x} = \frac{x_{\text{max}} - x_{\text{min}}}{2} $$
In questo contesto:
- \( x_{\text{max}} \) è il valore massimo registrato;
- \( x_{\text{min}} \) è il valore minimo registrato;
- \( e_{x} \) rappresenta l’errore assoluto della misura della grandezza \( x \).
Questo metodo si basa sull’idea che la variabilità dei dati rappresenti l’incertezza della misura: più i dati sono dispersi, maggiore è l’incertezza associata alla misura.
Perché la semidispersione è una buona stima dell’errore? L’idea alla base della semidispersione è semplice e intuitiva: un’alta variabilità dei valori misurati indica una maggiore incertezza. Se i dati sono molto concentrati attorno a un certo valore, la semidispersione sarà piccola, suggerendo un errore minore. Viceversa, se i dati sono molto distanti tra loro, la semidispersione aumenterà, segnalando una maggiore incertezza.
L'errore assoluto dipende anche dalla sensibilità dello strumento di misurazione (\( e_s \)), cioè la più piccola variazione misurabile dallo strumento utilizzato. Questa sensibilità rappresenta il limite minimo di precisione della misura.
- Se \( e_x > e_s \): quando l’errore assoluto \( e_x \), stimato tramite semidispersione, è maggiore della sensibilità dello strumento \( e_s \), è preferibile utilizzare la semidispersione come stima dell’errore, poiché rispecchia meglio la variabilità effettiva dei dati.
- Se \( e_x \le e_s \): se invece l’errore assoluto \( e_x \) è inferiore o uguale alla sensibilità \( e_s \), è più corretto adottare quest’ultima come errore assoluto, poiché le variazioni rilevate sono più piccole della precisione dello strumento e quindi meno affidabili.
Esempio pratico
Immagina di aver misurato una grandezza fisica \( x \) con uno strumento che ha una sensibilità di 0,1 cm.
Hai ottenuto i seguenti valori in cinque misurazioni:
$$ 2,4 \ \text{cm} \ , \ 2,5 \ \text{cm} \ , \ 2,7 \ \text{cm} \ , \ 2,6 \ \text{cm} \ , \ 2,4 \ \text{cm} $$
Calcola il valore medio dei dati:
$$ \bar{x} = \frac{2,4 + 2,5+ 2,7+2,6+2,4 }{5} = 2,52 \ \text{cm} $$
Il valore medio, però, non ti dice nulla sull'incertezza della misurazione. Per stimare l'incertezza del valore medio devi calcolare l'errore assoluto.
Individua il valore massimo e il valore minimo dei dati.
- Valore massimo \( x_{\text{max}} = 2,7 \)
- Valore minimo \( x_{\text{min}} = 2,4 \)
Poi calcola la semidispersione
$$ e_x = \frac{2,7 - 2,4}{2} = 0,15 \ \text{cm} $$
Ora confronta l'errore assoluto che hai appena calcolato con la sensibilità dello strumento di misura che hai usato.
La semidispersione $ e_x = 0,15 $ è maggiore della sensibilità dello strumento (0,1), quindi la stima migliore dell’errore assoluto è 0,15.
$$ x = \bar{x} \pm e_x $$
$$ x = 2,52 \pm 0,15 \ \text{cm} $$
Quindi, la misura dell'oggetto è compresa tra 2,52-0,15 cm e 2,52+0,15 cm.
$$ 2,52-0,15 \ \text{cm} < x < 2,52+0,15 \ \text{cm} $$
$$ 2,37 \ \text{cm} < x < 2,67 \ \text{cm} $$
Esempio 2
Considera lo stesso esempio di una serie di misurazioni, ma questa volta stai utilizzando uno strumento che ha una sensibilità di 0,5 cm. In altre parole, le tacche sul righello sono distanti mezzo centimetro tra loro anziché un millimetro.
Hai misurato una grandezza fisica \( x \) ottenendo i seguenti valori in cinque misurazioni:
$$ 2,4 \ \text{cm} \ , \ 2,5 \ \text{cm} \ , \ 2,7 \ \text{cm} \ , \ 2,6 \ \text{cm} \ , \ 2,4 \ \text{cm} $$
Sono gli stessi valori dell'esempio precedente.
Quindi, il valore medio è lo stesso.
$$ \bar{x} = \frac{2,4 + 2,5+ 2,7+2,6+2,4 }{5} = 2,52 \ \text{cm} $$
Anche l'errore assoluto basato sulla semidispersione è lo stesso.
$$ e_x = \frac{2,7 - 2,4}{2} = 0,15 \ \text{cm} $$
In questo caso, però, la semidispersione (0,15 cm) è minore della sensibilità dello strumento (0,5 cm).
Poiché l'errore assoluto stimato con la semidispersione (0,15 cm) è inferiore alla sensibilità dello strumento (0,5 cm), dovrai utilizzare la sensibilità dello strumento come errore assoluto.
$$ x = 2,52 \pm 0,5 \ \text{cm} $$
Questo perché la sensibilità rappresenta il limite minimo di precisione dello strumento, e le variazioni inferiori a 0,5 cm non possono essere considerate affidabili con questo strumento.
Quindi, il valore della grandezza è compreso tra 2,52-0,5 cm e 2,52+0,5 cm.
$$ 2,52-0,5 \ \text{cm} < x < 2,52+0,5 \ \text{cm} $$
$$ 2,02 \ \text{cm} < x < 3,02 \ \text{cm} $$
In altre parole, l'errore assoluto per questa serie di misurazioni sarà 0,5 cm, la sensibilità dello strumento, poiché le variazioni nei dati sono al di sotto della precisione consentita dal metro.
Quando non conviene utilizzare la semidispersione?
Quando fai tante misurazioni, la semidispersione può essere influenzata da valori anomali sporadici e fuori scala, ossia da misure estreme rilevate per caso o per errore, e rischia di dare una stima poco affidabile della dispersione.
Ad esempio, supponiamo di misurare la temperatura in un ambiente e otteniamo i seguenti valori in gradi Celsius: $$
20.1, \quad 20.3, \quad 20.2, \quad 20.4, \quad 20.2, \quad 25.0 $$ In questo caso, il valore 25.0 è un'anomalia evidente rispetto agli altri, probabilmente dovuta a un errore di misura o a una variazione momentanea non rappresentativa dell'andamento generale. Se calcoliamo la semidispersione massima usando questi dati, il valore dipenderà in gran parte dagli estremi \(20.1\) e \(25.0\), e quindi potrebbe sovrastimare la dispersione effettiva. $$ e_x = \frac{25.0 - 20.1}{2} = 2.45 $$ Quindi, considerando che la media dei valori è $ \bar{x} = 21.0 \ \text{cm} $ l'errore assoluto diventa troppo ampio $$ x = 21.0 \pm 2.45 \ \text{cm} $$
In questi casi, è meglio usare lo scarto quadratico medio (o deviazione standard) per calcolare la dispersione dei valori intorno alla media e l'incertezza dei dati.
La devianza standard è un indicatore migliore perché tiene conto di tutti i valori raccolti, non solo degli estremi.
Quindi, ti fornisce una misura più rappresentativa della dispersione dei valori intorno alla media e dell'incertezza dei dati.
Ad esempio, calcolando la deviazione standard (o scarto quadratico medio) sui dati dell'esempio precedente, otterremo un valore che tiene conto di tutti i valori. Quindi sarà meno influenzato dall'anomalia fuori scala (25.0°). La deviazione standard risulterà più rappresentativa della vera dispersione intorno alla media dei valori tipici ($ \bar{x} = 21.0°C $). $$ \sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \overline{x})^2} $$ $$ \sigma = \sqrt{\frac{1}{6} \cdot [(20.1-21)^2+(20.3-21)^2+ ... + (25-21)^2 ]} $$ $$ \sigma = \sqrt{\frac{1}{6} \cdot 19.99} $$ $$ \sigma = \sqrt{3.33} $$ $$ \sigma = 1.82 \ \text{cm} $$ Quindi, lo scarto quadratico medio è circa 1.82 cm. $$ x = 21.0 \pm 1.82 \ \text{cm} $$ In questo caso l'errore assoluto (1.82 cm) è inferiore rispetto a quello calcolato con la semidispersione (2.45 cm).
Le cifre significative dell'errore assoluto
L'errore assoluto deve essere sempre arrotondato a una o due cifre significative, per evitare di dare troppa precisione a qualcosa che è, appunto, un errore.
L'idea è di non illudere nessuno su un livello di precisione che in realtà non c’è..
In ogni caso, l'ultima cifra significativa del valore attendibile (valore misurato) deve essere dello stesso ordine di grandezza dell'errore, ossia nella stessa posizione decimale, per mantenere una coerenza decimale.
Ad esempio se hai un errore di 0,02 cm, vuol dire che la precisione della misura si ferma ai centesimi. Di conseguenza, devi anche limitare il valore misurato alla stessa precisione, ossia ai centesimi, per mostrare correttamente il livello d’incertezza.
Esempio
Supponiamo che tu stia misurando la lunghezza di un oggetto con un righello di precisione e ottieni questi valori:
- Valore misurato: \( 12,346 \) cm
- Errore assoluto: \( 0,05 \) cm
L’errore \( 0,05 \) cm ha come ultima cifra significativa la posizione decimale dei centesimi.
Ora, per seguire la regola di coerenza decimale, devi arrotondare il valore misurato alla stessa posizione decimale dell’errore, ossia ai centesimi.
Quindi, da \( 12,346 \) cm, il valore misurato si arrotonda a \( 12,35 \) cm.
In conclusione puoi scrivere il risultato in modo coerente, combinando valore ed errore così:
$$ \text{Lunghezza} = (12,35 \pm 0,05) \, \text{cm} $$
Arrotondando il valore misurato alla stessa posizione decimale dell'errore, hai un risultato che rispetta la precisione della misura, senza dare l'impressione di una precisione eccessiva o ingannevole.
Come rappresentare gli errori assoluti delle misure in un grafico
Gli errori assoluti si rappresentano utilizzando segmenti perpendicolari agli assi che partono dai punti dei valori misurati:
- I segmenti orizzontali indicano l'incertezza della misura sull'ascissa (asse \(x\)).
- I segmenti verticali rappresentano l'incertezza della misura sull'ordinata (asse \(y\)).
La lunghezza di ciascun segmento rappresenta il range dell'errore assoluto. Si calcola come la differenza tra il valore massimo e il valore minimo della misura, considerando l'errore.
Ad esempio, se una misura \( x \) ha un errore assoluto di \( \pm 0.2 \), il segmento orizzontale sull'ascissa si estenderà da \( x - 0.2 \) a \( x + 0.2 \).
Questi segmenti mostrano chiaramente la variazione possibile dei valori misurati dovuta agli errori.
Un esempio pratico
Immaginiamo di misurare l'altezza (\(y\)) e il peso (\(x\)) di tre persone, sapendo che ogni misura ha un errore assoluto specifico. Ecco i dati:
| Persona | Peso (x) [kg] | Errore Assoluto (±) | Altezza (y) [cm] | Errore Assoluto (±) |
|---|---|---|---|---|
| A | 70 | 2 | 175 | 3 |
| B | 65 | 1.5 | 180 | 2 |
| C | 80 | 3 | 170 | 4 |
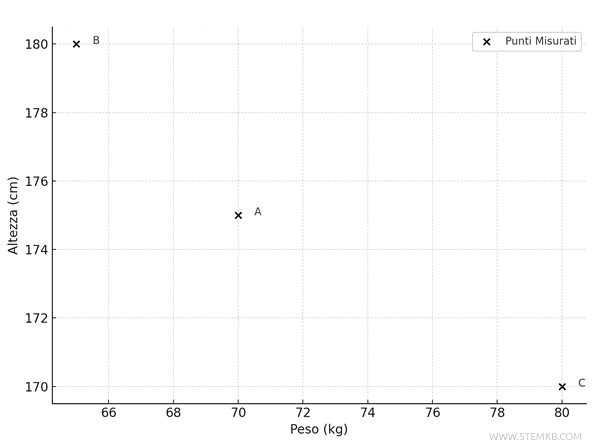
I punti associati ai valori attendibili nel grafiico sono i seguenti:
- Persona A: \( (70, 175) \),
- Persona B: \( (65, 180) \),
- Persona C: \( (80, 170) \).
Questi punti però non ci dicono nulla sull'errore assoluto delle misure.
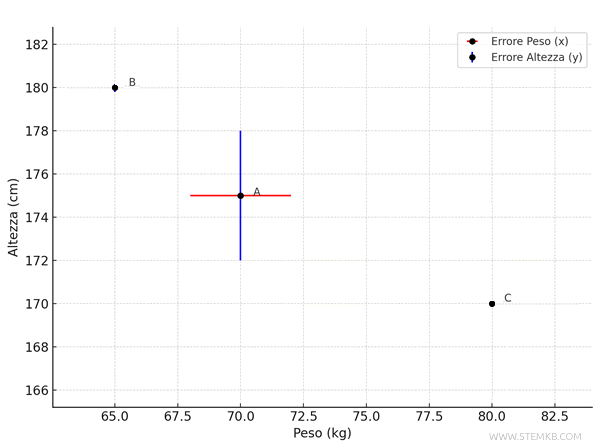
Per considerare anche l'errore assoluto, a ciascun punto del grafico aggiungiamo dei segmenti perpendicolari agli assi rappresentano l'intervallo di errore:
- Persona A (\(x = 70\), \(y = 175\)):
- Peso (\(x\)): errore assoluto di \( \pm 2 \), quindi il segmento orizzontale va da \( 70 - 2 = 68 \) a \( 70 + 2 = 72 \).
- Altezza (\(y\)): errore assoluto di \( \pm 3 \), quindi il segmento verticale va da \( 175 - 3 = 172 \) a \( 175 + 3 = 178 \).
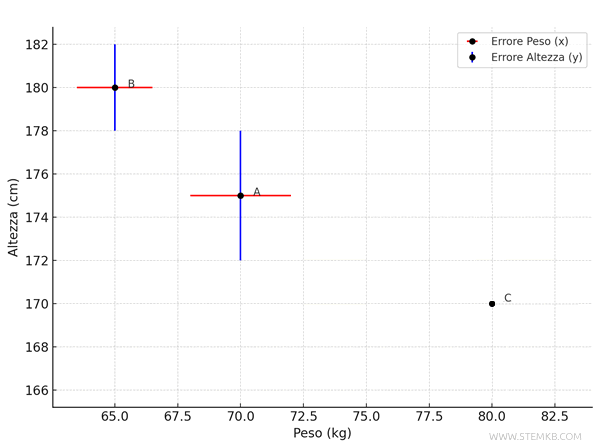
- Persona B (\(x = 65\), \(y = 180\)):
- Peso (\(x\)): errore assoluto di \( \pm 1.5 \), quindi il segmento orizzontale va da \( 65 - 1.5 = 63.5 \) a \( 65 + 1.5 = 66.5 \).
- Altezza (\(y\)): errore assoluto di \( \pm 2 \), quindi il segmento verticale va da \( 180 - 2 = 178 \) a \( 180 + 2 = 182 \).
- Persona C (\(x = 80\), \(y = 170\)):
- Peso (\(x\)): errore assoluto di \( \pm 3 \), quindi il segmento orizzontale va da \( 80 - 3 = 77 \) a \( 80 + 3 = 83 \).
- Altezza (\(y\)): errore assoluto di \( \pm 4 \), quindi il segmento verticale va da \( 170 - 4 = 166 \) a \( 170 + 4 = 174 \).
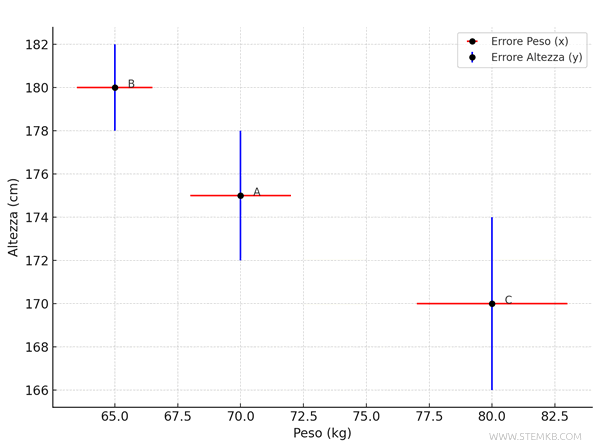
Adesso il grafico che rappresenta i dati di altezza e peso delle tre persone include anche gli errori assoluti.
I segmenti orizzontali (peso) e verticali (altezza) che passano per i rispettivi punti hanno una lunghezza proporzionale agli errori assoluti e misurano l'incertezza delle misure.
In questo modo il grafico offre anche una chiara visione delle possibili variazioni dovute agli errori di misura.
La rappresentazione grafica degli errori assoluti è molto utile, perché ti permette di visualizzare l'incertezza associata a una misura e aiuta a comprendere a colpo d'occhio la precisione dei dati.