I postulati di Euclide
I postulati di Euclide costituiscono le fondamenta della geometria euclidea. Sono un insieme di affermazioni di base, assiomi e postulati da cui si possono dedurre tutti gli altri teoremi e proprietà geometriche.
Euclide è stato un matematico greco, attivo ad Alessandria d'Egitto intorno al 300 a.C., noto soprattutto per il suo lavoro "Elementi", un'opera composta in 13 libri che coprono un'ampia gamma di argomenti matematici.
Questo trattato è una delle opere più influenti nella storia della matematica, e ha costituito la base dell'insegnamento della geometria per oltre due millenni.
Il contenuto degli Elementi di Euclide.
- Libri I-VI: Trattano principalmente di geometria piana e teoremi fondamentali come il teorema di Pitagora.
- Libri VII-IX: Si concentrano sulla teoria dei numeri, includendo la discussione sui numeri primi e la famosa procedura per trovare il massimo comune divisore.
- Libro X: Affronta la teoria delle proporzioni irrazionali.
- Libri XI-XIII: Esplorano la geometria solida, la classificazione dei poliedri regolari, noti come solidi platonici.
Il metodo utilizzato da Euclide è quello assiomatico-deduttivo, dove parte da un insieme di assiomi e postulati fondamentali per dedurre teoremi e costruzioni geometriche in modo logico e rigoroso.
- Gli assiomi sono affermazioni fondamentali considerate evidenti di per sé, che non richiedono dimostrazione e servono come base per costruire un sistema logico.
- I postulati, simili agli assiomi, sono proposizioni specifiche utilizzate come punti di partenza per dedurre e dimostrare teoremi all'interno di un particolare contesto o sistema, come la geometria.
L'approccio sistematico e rigoroso di Euclide ha reso "Elementi" un testo fondamentale non solo per la matematica, ma anche per lo sviluppo del pensiero logico e scientifico in generale.
I cinque postulati di Euclide
Euclide formulò cinque postulati nel suo trattato "Elementi".
- Postulato della retta
Per due punti distinti passa una e una sola retta.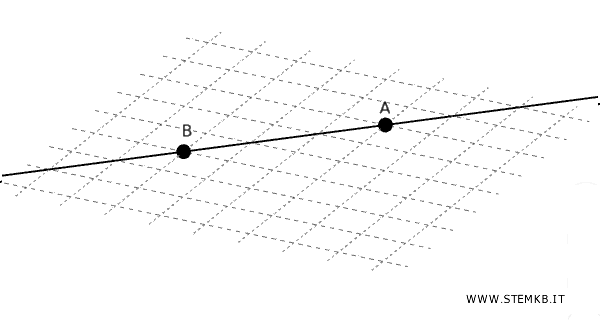
Esempio: Se hai due punti A e B su un foglio, esiste un'unica linea retta che li collega.
- Postulato dell'estensione
Un segmento di linea retta AB può essere esteso indefinitamente in entrambe le direzioni.
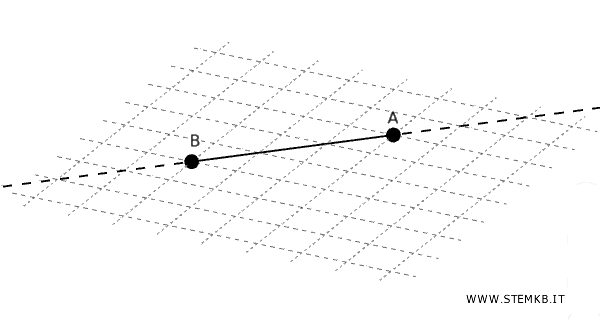
Esempio. Se disegni un segmento di retta tra i punti A e B, puoi continuare a disegnare la linea in entrambe le direzioni senza limiti.
- Postulato del cerchio
Dato un punto P e una distanza r, è sempre possibile tracciare un cerchio con quel punto P come centro e quella distanza r come raggio.
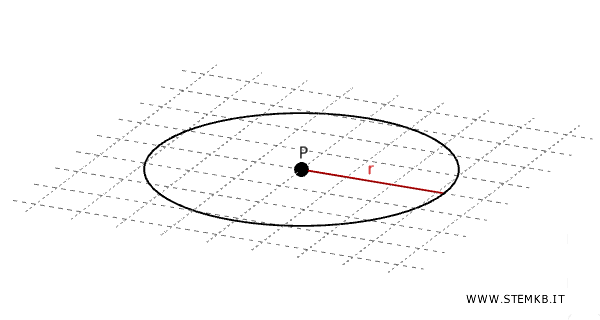
Esempio. Se hai un punto A e una lunghezza di 5 cm, puoi disegnare un cerchio con il centro in A e un raggio di 5 cm.
- Postulato dell'angolo retto
Tutti gli angoli retti sono uguali tra loro.
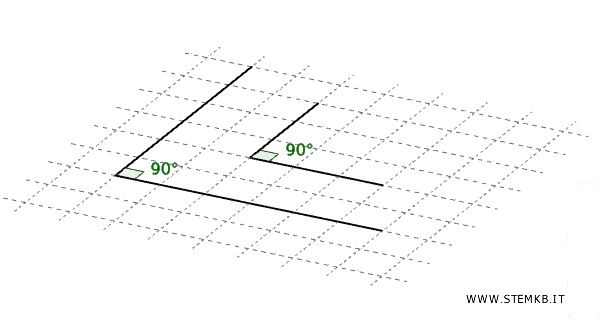
Esempio. Se disegni due angoli retti su un foglio, indipendentemente dalla loro posizione o orientamento, entrambi misureranno sempre 90 gradi.
- Postulato delle parallele
Data una retta e un punto non appartenente ad essa, esiste una e una sola retta parallela alla prima passante per quel punto.
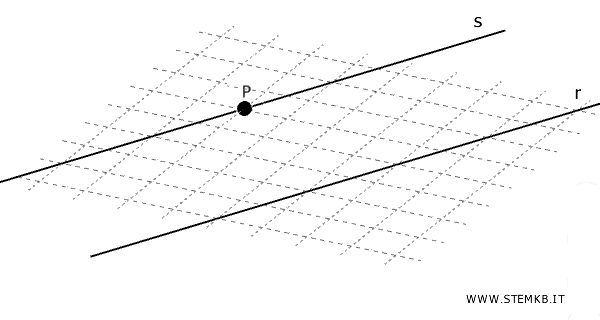
Esempio. Se hai una retta r e un punto P non appartenente a r, esiste un'unica retta s che passa per P e non interseca mai r, ovvero è parallela a r.
Questi postulati sono essenziali perché, a partire da essi, Euclide è stato in grado di sviluppare un sistema di geometria che è rimasto fondamento della matematica per secoli.
Utilizzando solo questi cinque postulati e la logica deduttiva, Euclide ha dimostrato numerosi teoremi e ha costruito una struttura geometrica rigorosa detta geometria euclidea (o geometria piana).
I postulati di Euclide non solo definiscono i concetti fondamentali della geometria euclidea, ma forniscono anche un metodo per esplorare e comprendere le proprietà dello spazio. Sono un esempio di come una base solida e ben definita possa portare a una vasta e profonda teoria matematica.