La retta

ogni retta è un sottoinsieme del piano perché tutti i punti della retta appartengono al piano in cui essa giace. Questo significa che una retta è parte di un piano e non può esistere al di fuori di esso nella geometria euclidea.n geometria, una retta è un insieme infinito di punti disposti in modo tale che, dati due qualsiasi punti appartenenti alla retta, il segmento che li congiunge giace interamente sulla retta stessa.

 

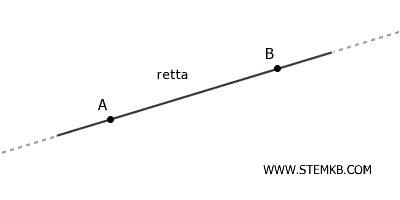
Si tratta di una delle figure geometriche fondamentali ed è uno dei concetti base della geometria euclidea.

Una linea retta ha lunghezza ma non ha larghezza o spessore.

E' illimitata nell'estensione. Può essere estesa in entrambe le direzioni indefinitamente.

 

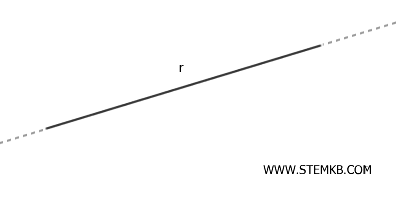
In genere è designata dalle lettere maiuscole di qualsiasi due dei suoi punti (es. A, B) o da una lettera minuscola (r),

Fai attenzione a non confondere la retta con il segmento o la semiretta. Sono concetti diversi.

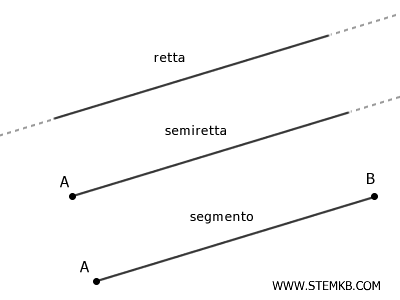
Mentre la retta si estende all'infinito in entrambe le direzioni, il segmento ha una lunghezza finita e la semiretta ha un punto di partenza ma si estende all'infinito in una sola direzione.

Il concetto di retta, così come altri concetti geometrici fondamentali, è stato studiato e formalizzato per la prima volta dagli antichi greci, in particolare da Euclide nel suo trattato "Gli Elementi". Da allora, la comprensione e l'applicazione delle rette è cresciuta e si è evoluta, giocando un ruolo cruciale nello sviluppo della matematica e della scienza nel suo complesso.

Le proprietà della retta

Una retta sul piano ha le seguenti proprietà:

• Tra due punti distinti del piano passa una sola retta.
  
• Una retta contiene un numero infinito di punti.
• Se due punti appartengono a una retta, allora tutti i punti compresi tra di loro appartengono anch'essi alla retta.
• Tutti i punti di una retta giacciono sullo stesso piano.

L'equazione della retta

In uno spazio bidimensionale, come il piano cartesiano, l'equazione generale di una retta è data da

$$ Ax+By+C=0 $$

Dove A, B, e C sono coefficienti costanti e almeno uno tra A e B è non nullo.

Inoltre, se conosci il coefficiente angolare m e l'intercetta q, puoi rappresentare la retta anche con un'equazione in questa forma

$$ y=mx $$

Le rette incidenti, parallele e coincidenti

Due rette nel piano possono avere una delle seguenti posizioni relative:

• Rette incidenti
  Sono rette che si intersecano in un punto P in comune.
  
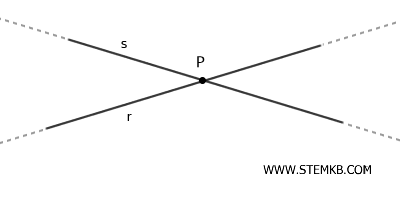
• Parallele
  Sono rette che non hanno alcun punto in comune.
  
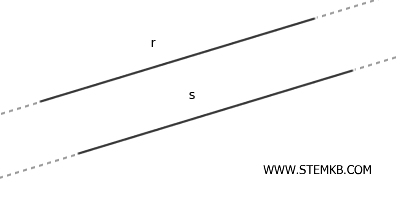
• Coincidenti
  Sono rette che hanno tutti i punti in comune. Quindi, sono la stessa retta.

La retta orientata

Una retta orientata è una retta su cui è stato fissato un verso di percorrenza, il che permette di stabilire un ordine tra i punti in base alla direzione scelta (ad esempio, da sinistra a destra o viceversa).

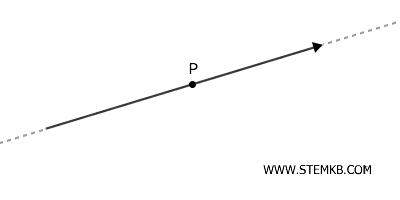
Questo implica che, dato un punto \( P \) sulla retta, possiamo decidere un verso di percorrenza, verso destra o verso sinistra, che definisce il modo in cui osserviamo la successione dei punti.

La caratteristica principale di una retta orientata è che ci consente di fissare un ordine tra i punti.

Quando la retta è orientata, i punti \( A \) e \( B \) della retta possono essere ordinati in base al verso di percorrenza.

• Se \( A \) si trova prima di \( B \) nel verso di percorrenza della retta orientata, diciamo che \( A \) precede \( B \).
  
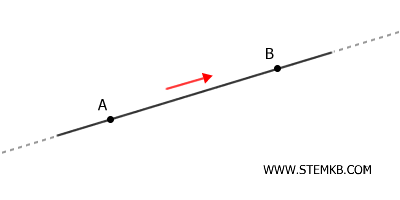
• Se \( B \) si trova prima di \( A \) nel verso della retta orientata, allora \( B \) precede \( A \).
  

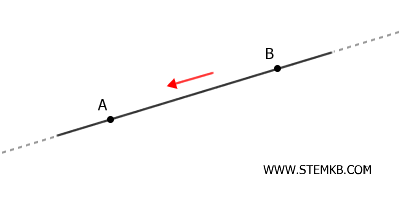
Questo concetto trova applicazioni in geometria analitica e fisica, ad esempio per definire i vettori o per rappresentare fenomeni in cui la direzione è significativa (come il moto lungo un asse).

Il fascio di rette

Un fascio proprio di rette è l'insieme di tutte le rette che passano per un punto comune \( P \), detto centro del fascio.

Ad esempio, se consideriamo un punto \( P \) in un piano, ogni retta del fascio può essere definita da un'inclinazione o pendenza diversa, ma tutte passeranno per \( P \).

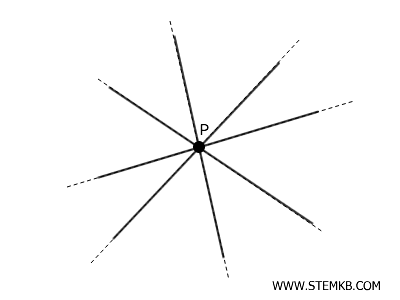
Le rette del fascio si dispongono in modo da coprire tutte le direzioni possibili a partire dal punto \( P \).

E' un concetto fondamentale per studiare le relazioni geometriche tra le rette e gli angoli.

Gli assiomi della retta nella geometria euclidea

Gli assiomi di appartenenza della retta enunciati sopra fanno parte della geometria euclidea e stabiliscono le relazioni fondamentali tra punti e rette. Vediamoli con un esempio pratico per chiarirli:

• Ogni retta è un sottoinsieme del piano
  Ogni retta è un sottoinsieme del piano perché tutti i punti della retta appartengono anche al piano in cui la retta giace. Questo significa che una retta è parte di un piano e non può esistere al di fuori di esso nella geometria euclidea.
  
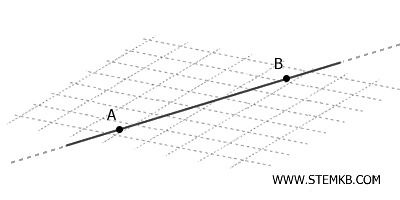
• A ogni retta appartengono almeno due punti distinti
  Questo significa che una retta non può essere definita con meno di due punti. Ad esempio, se disegni una retta \( r \), possiamo sempre individuare due punti distinti, \( A \) e \( B \), appartenenti a \( r \).
  
• Dati due punti distinti esiste una e una sola retta alla quale appartengono entrambi
  Questo assioma implica che i due punti determinano univocamente una retta. Se prendi due punti distinti \( A \) e \( B \), esiste una sola retta \( r \) che passa per entrambi.

  Da questo possiamo dedurre che due rette distinte sul piano possono avere in comune al massimo un punto. Se avessero in comune due o più punti, tra questi punti passerebbe una sola retta, quindi le due rette sarebbero rette coincidenti.

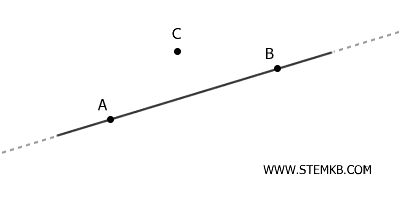
• Data una retta nel piano, esiste almeno un punto del piano che non appartiene a essa
  Questo assioma chiarisce che una retta non può contenere tutti i punti del piano; il piano è infatti composto da un numero infinito di punti, non tutti situati sulla stessa retta.
  
• Gli assiomi d'ordine della retta
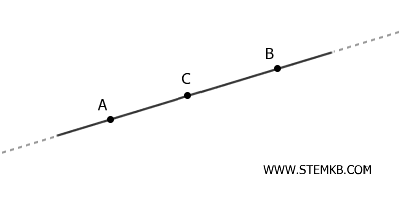
  Gli assiomi d'ordine della retta stabiliscono le proprietà fondamentali che regolano l'ordine tra i punti di una retta. Questi assiomi possono essere sintetizzati come segue:
  • Assioma di esistenza del punto intermedio
    Dati due punti distinti \( A \) e \( B \) su una retta, esiste sempre un punto \( C \) compreso tra \( A \) e \( B \). Questo implica che la retta è densa, ovvero tra due punti qualsiasi è possibile trovare infiniti altri punti.
    
  • Assioma di estensione
    Dato un punto \( P \) su una retta, esistono sempre almeno due punti \( A \) e \( B \) tali che \( A \) precede \( P \) e \( P \) precede \( B \). Questo implica che la retta si estende all'infinito in entrambe le direzioni, senza confini.
    

  Da questi assiomi deduciamo l'infinitezza e la continuità dell'insieme dei punti su una retta.

Questi assiomi costituiscono le basi della geometria piana e ci permettono di costruire ulteriori concetti come angoli, triangoli, e altre figure geometriche.