Problema di geometria triangoli 2

Dato un triangolo ABC in cui sono tracciate le bisettrici degli angoli ai vertici A e B, se l'angolo $ A \hat{C} B $ ha un'ampiezza di 56°, quanto vale l'ampiezza dell'angolo x e y?

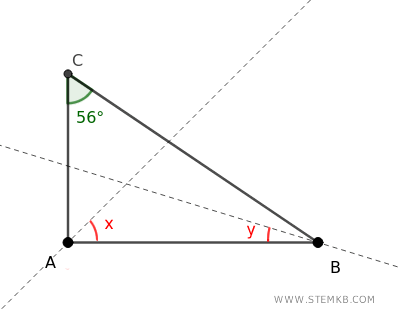
Soluzione svolta

Il triangolo è un triangolo rettangolo perché l'angolo al vertice $ B \hat{A} C $ è un angolo retto (90°).

Poiché la bisettrice divide un angolo a metà, puoi già dedurre che l'angolo x è la metà di 90° ossia 45°

$$ x = 45° $$

Se ricordi bene, la somma degli angoli interni di un triangoli è sempre uguale a 360°.

$$ A \hat{B} C + B \hat{A} C + A \hat{C} B =180° $$

Sostituisci le ampiezze degli angoli che conosci.

$$ A \hat{B} C + 90° + 56° =180° $$

In questo modo trovi l'ampiezza dell'angolo $ A \hat{B} C $

$$ A \hat{B} C =180° - 90° - 56°$$

$$ A \hat{B} C = 34°$$

La bisettrice divide a metà l'angolo $ A \hat{B} C $, quindi puoi dedurre che l'angolo y é la metà di 34° ossia 17°.

$$ y = 17° $$

A questo punto devi solo sommare le due ampiezze x e y che hai appena trovato.

$$ x + y = 45° + 17° $$

$$ x + y = 62° $$

Pertanto la soluzione del problema è x+y=62°