Segmento in geometria
Il segmento è un concetto basilare in geometria. Immagina una linea retta tra due punti A e B: questo è un segmento.
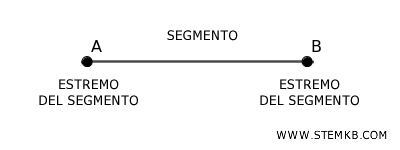
I due punti sono gli "estremi" del segmento. La lunghezza del segmento è la distanza tra questi punti.

Quindi, un segmento è una parte di una linea retta limitata da due estremi. A differenza di una linea, che continua all'infinito, un segmento ha una fine e un inizio ben definiti.

Perché è importante capire bene cos'è un segmento?
I segmenti sono fondamentali in geometria. Formano i lati dei poligoni e sono alla base di molte strutture geometriche.
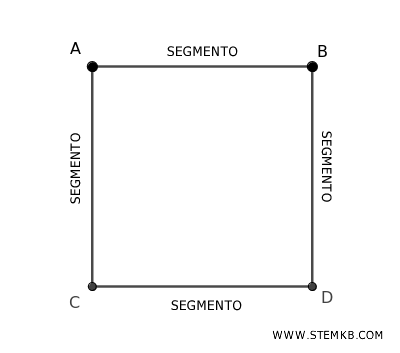
Ad esempio, ogni lato di un poligono è un segmento. Se consideri un quadrato, questo è formato da quattro segmenti adiacenti consecutivi tra loro.
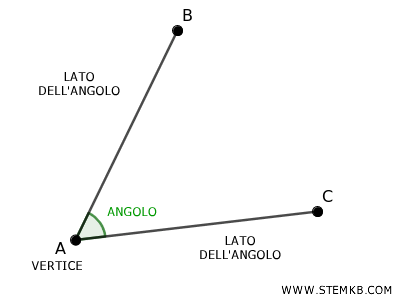
Anche gli angoli sono formati dall'intersezione di due segmenti.
Inoltre, i segmenti hanno molte applicazioni pratiche in svariati campi, come l'ingegneria, l'architettura, e il disegno tecnico.
Quindi, per comprendere le forme geometriche più complicate devi avere ben chiaro cos'è un segmento.
Come si misura un segmento
Se ti chiedono di misurare un segmento, devi calcolare la distanza tra i suoi estremi A e B.
Puoi usare un righello, le squadre o altri strumenti di misurazione di precisione come il calibro.
La lunghezza può essere calcolata anche matematicamente, tramite le formule geometriche, soprattutto se il segmento è parte di una figura più complessa. Ad esempio, per trovare la lunghezza di un lato di un quadrato, se conosci già il perimetro puoi semplicemente dividere il perimetro del quadrato per 4. E' un esempio banale... ma rende l'idea che non sempre occorre misurare fisicamente un segmento.
Le proprietà dei segmenti
Ogni segmenti soddisfa alcune proprietà geometriche. Eccone alcune:
- Un segmento è una parte di una linea retta. Quindi, una linea curva non può essere un segmento.
- Il prolungamento di un segmento. Ogni segmento può essere prolungato in entrambi gli estremi A e B da una semiretta. Ad esempio, la semiretta \( s \) che ha origine da B appartiene alla retta AB ma non contiene il punto A.

Viceversa, la semiretta \( s \) che ha origine da A appartiene sempre alla retta AB ma non contiene il punto B.

- Un segmento ha una lunghezza finita e costante che puoi calcolare utilizzando i suoi estremi. Si distingue da una linea retta, che invece si estende all'infinito in entrambe le direzioni.

- Pur essendo una parte finita di una retta, ogni segmento è composto da infiniti punti.
Spiegazione. Riflettendo sulla natura del segmento in geometria, possiamo formulare un'affascinante osservazione: pur essendo una frazione finita di una linea retta, ogni segmento racchiude in sé un insieme di punti infinitamente vasto. Se prendi due punti distinti qualsiasi lungo un segmento, tra essi ci sono innumerevoli altri punti intermedi. Quindi, in un singolo segmento c'è l'incredibile realtà di un universo di punti senza fine, un continuum che unisce i due estremi.
Tipi di segmenti
Esistono diversi tipi di segmenti, vediamone alcuni per imparare un po' di terminologia.
- Segmenti congruenti
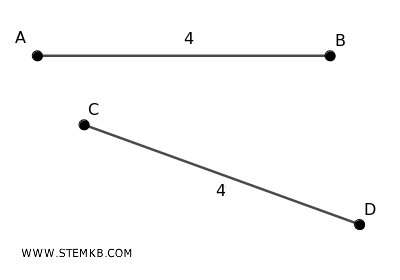
Due segmenti sono congruenti se hanno la stessa lunghezza. Non occorre che abbiano anche la stessa direzione. Possono anche avere inclinazioni diverse. Puoi considerarli come gemelli della lunghezza.
- Segmenti consecutivi
Due segmenti AB e AC sono detti consecutivi se hanno uno e un solo estremo in comune.
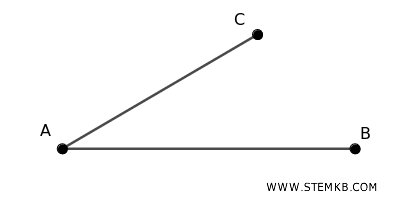
- Segmenti adiacenti
Due segmenti AB e AC sono adiacenti se hanno uno e un solo estremo in comune (sono consecutivi) e appartengono alla stessa retta.
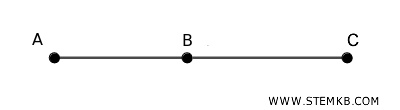
- Segmento nullo
Un segmento AB è detto "nullo" nel caso particolare in cui gli estremi A e B coincidono. - Segmenti incidenti
Due segmenti sono detti incidenti se hanno un punto qualsiasi in comune.
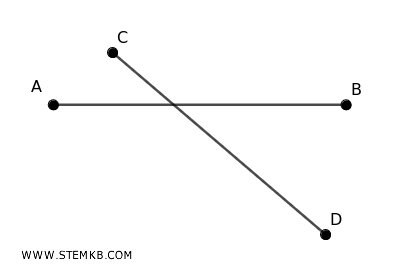
- Segmenti perpendicolari
Due segmenti sono perpendicolari quando hanno un punto in comune in comune formando quattro angoli retti (perpendicolari) ossia quattro angoli di 90°.
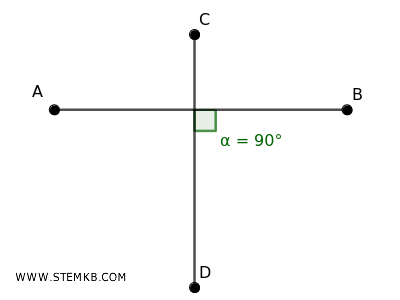
- Segmenti paralleli
Due segmenti sono paralleli se non si incontrano mai e hanno la stessa direzione, ossia la stessa distanza in ogni loro punto.
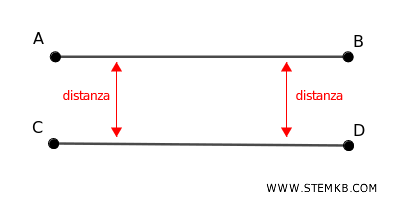
Il confronto tra segmenti
Il confronto tra due o più segmenti ci consente di stabilire relazioni di lunghezza tra i segmenti.
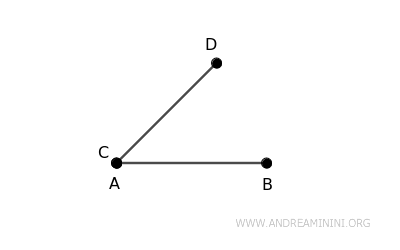
Prendiamo due segmenti \( AB \) e \( CD \)

Spostiamo il segmento \( CD \) facendo coincidere i punti \( A \) e \( C \), in questo modo i due segmenti hanno un estremo condiviso.
Dopo lo spostamento i due segmenti sono congruenti con quelli di origine perché hanno la stessa lunghezza.
Se ora tracciamo una semiretta con origine \( A \) contenente il punto \( B \), possiamo individuare un punto \( P \) sulla semiretta in modo che il segmento \( AP \) sia congruente a un segmento dato \( CD \) ossia \( AP \cong CD \)
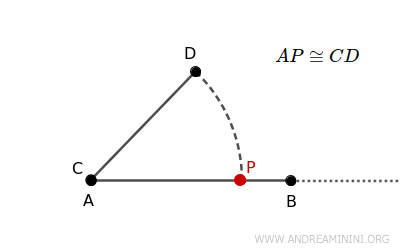
Questo punto \( P \) ci permette di confrontare \( AB \) e \( CD \), in funzione della posizione di \( P \) rispetto al segmento \( AB \)
Dal confronto possono emergere tre scenari, ognuno associato a una diversa relazione tra i segmenti \( AB \) e \( CD \)
- Il punto \( P \) cade esternamente al segmento \( AB \)
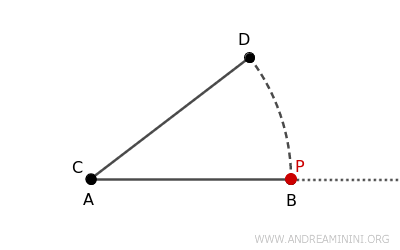
In questo caso, il punto \( P \) si trova oltre il punto \( B \) sulla semiretta. Quindi, il segmento \( AP \) è più lungo del segmento \( AB \). $$ AP>AB $$ Ciò significa che la lunghezza del segmento \( CD \) è maggiore di quella di \( AB \) $$ AB < CD $$Ad esempio, se \( AB = 4 \, \text{cm} \) e \( CD = 5 \, \text{cm} \), il punto \( P \) si troverà a 5 cm da \( A \), esternamente a \( B \).
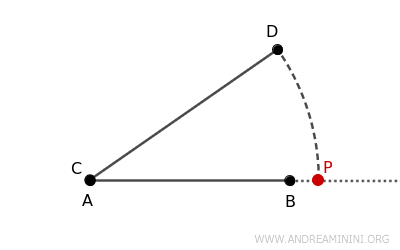
- Il punto \( P \) coincide con il punto \( B \)
Se \( P \) coincide esattamente con \( B \), i due segmenti hanno la stessa lunghezza e si definiscono congruenti. $$ AP \cong AB $$ Quindi, poiché \( AP \cong CD \), anche i segmenti \( AB \) e \( CD \) sono congruenti $$ AB \cong CD $$Ad esempio, se \( AB = 4 \, \text{cm} \) e \( CD = 4 \, \text{cm} \), il punto \( P \) coinciderà con il punto \( B \), dimostrando che \( AB \) e \( CD \) sono equivalenti.
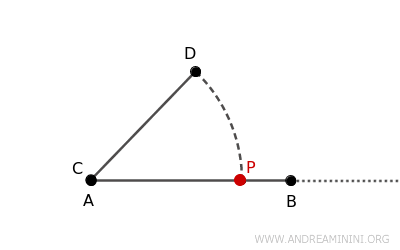
- Il punto \( P \) cade internamente al segmento \( AB \)
Infine, se \( P \) si trova tra \( A \) e \( B \), il segmento \( AP \) è più corto di \( AB \). $$ AP<AB $$ In questo caso, il segmento \( AB \) è più lungo di \( CD \), poiché quest'ultimo è congruente con \( AP \) $$ AB > CD $$Ad esempio, se \( AB = 6 \, \text{cm} \) e \( CD = 4 \, \text{cm} \), il punto \( P \) si troverà a 4 cm da \( A \), all'interno del segmento \( AB \).
La somma dei segmenti
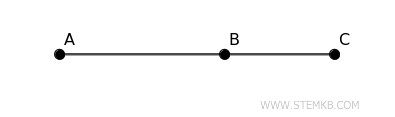
Se consideriamo due segmenti adiacenti, \( AB \) e \( BC \), la loro somma corrisponde semplicemente al segmento \( AC \) che li unisce.
$$ AB + BC = AC $$
Ma cosa succede se i segmenti non sono adiacenti? In questo caso, entra in gioco il concetto di congruenza, ossia la sovrapposizione perfetta tra segmenti di uguale lunghezza.
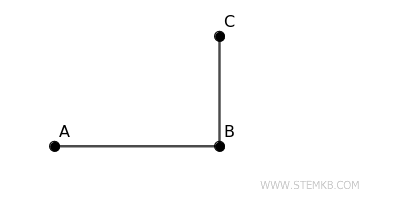
La somma di due segmenti non adiacenti \( AB \) e \( BC \) non adiacenti si ottiene immaginando due segmenti congruenti a \( AB \) e \( BC' \), posizionati in modo adiacente dove \( BC \cong BC' \) sono segmenti congruenti.
Il segmento risultante \( AB + BC' = AC' \) rappresenta la loro somma.
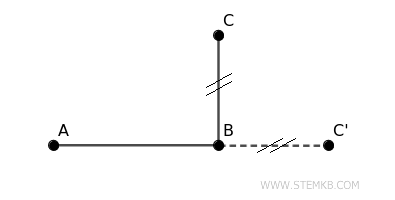
Questa proprietà può essere estesa a più segmenti: la somma di \( AB \), \( CD \) e \( EF \) si ottiene indipendentemente dall’ordine in cui si combinano i segmenti.
Allo stesso modo la differenza tra due segmenti \( AB \) e \( CD \) è definita come il segmento che, sommato a \( CD \), restituisce \( AB \). Se \( CD \) è minore o uguale a \( AB \), la differenza si indica con \( AB - CD = BP \). In pratica, stiamo individuando il tratto mancante per completare \( AB \) a partire da \( CD \).
Multipli e sottomultipli di segmenti
Quando sommiamo un segmento \( AB \) a se stesso \( n \) volte, otteniamo un segmento \( CD \) che rappresenta un multiplo di \( AB \):
$$ CD = n \cdot AB $$
In modo simile, possiamo dire che \( AB \) è un sottomultiplo di \( CD \) se \( CD \) può essere diviso in \( n \) parti congruenti tra loro e uguali a \( AB \):
$$ AB = \frac{1}{n} CD $$
Questo concetto si estende anche a rapporti frazionari. Quindi, se scriviamo \( CD = \frac{m}{n} AB \), stiamo dicendo che \( CD \) equivale alla somma di \( m \) segmenti ciascuno lungo \( \frac{1}{n} AB \).
In conclusione, il segmento è un concetto semplice ma potente in geometria. Serve a comprendere forme e strutture complesse e ha molte applicazioni pratiche. Capirlo bene è un passo fondamentale nell'apprendimento della geometria.
Segmenti commensurabili e incommensurabili
Due segmenti si dicono commensurabili quando il rapporto tra le loro lunghezze può essere espresso come un numero razionale \( \frac{a}{b} \).
In termini pratici, significa che esiste un’unità di misura comune che permette di esprimere entrambe le lunghezze come multipli interi di questa unità.
Possiamo pensare al caso come a una situazione in cui entrambi i segmenti possono essere suddivisi in pezzi più piccoli della stessa lunghezza, che rappresenta la loro unità di misura comune.
Un esempio semplice ed efficace è dato da due segmenti lunghi rispettivamente 12 cm e 18 cm.
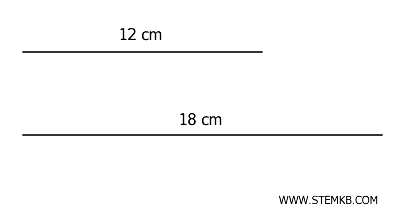
Il rapporto tra le loro lunghezze è: $$ \frac{12}{18} = \frac{2}{3} $$ Essendo \( \frac{2}{3} \) un numero razionale, possiamo affermare che questi segmenti sono commensurabili. Per trovare l'unità di misura in comune basta calcolare il massimo comune divisore dei due numeri che, in questo caso, è 6 cm. $$ MCD(12,18) = 6 $$ Quindi, entrambi i segmenti possiamo scomporli in segmenti più piccoli di 6 cm.
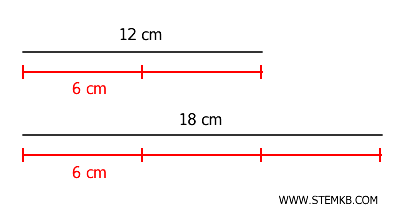
Due segmenti diventano incommensurabili quando non possono essere descritti come multipli interi di una stessa unità di misura, perché il rapporto tra le loro lunghezze è un numero irrazionale.
Questo significa che non esiste una frazione \( \frac{p}{q} \), con \( p \) e \( q \) numeri interi, che descriva esattamente il rapporto tra i segmenti.
Un esempio classico è il rapporto tra il lato e la diagonale di un quadrato. Se il lato del quadrato ha lunghezza \( 1 \), grazie al teorema di Pitagora \( \sqrt{1^2+1^2} \) sappiamo che la diagonale avrà lunghezza \( \sqrt{2} \).
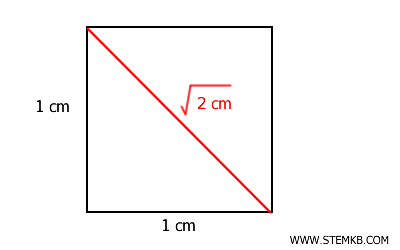
Il rapporto tra un lato e la diagonale è dunque: $$ \frac{\text{lato}}{\text{diagonale}} = \frac{1}{\sqrt{2}} $$ Poiché \( \sqrt{2} \) è un numero irrazionale, non esiste un’unità di misura comune per il lato e la diagonale. Questo esempio, che risale ai pitagorici, è uno dei primi incontri storici con i numeri irrazionali.
La scoperta dei segmenti incommensurabili fu un evento epocale
I pitagorici, che basavano la loro visione del mondo sull’armonia e sulle proporzioni razionali, rimasero sconvolti da questa scoperta.
Si racconta che la consapevolezza dell'esistenza dei numeri irrazionali fosse inizialmente mantenuta segreta, quasi fosse un pericolo per l'ordine cosmico.
Con il tempo, però, i matematici abbracciarono questa nuova realtà e svilupparono strumenti per comprendere e lavorare con i numeri irrazionali. Da allora, i numeri come \( \pi \), \( e \) e \( \sqrt{2} \) sono diventati pilastri fondamentali della matematica moderna.