Le figure geometriche

Una figura geometrica è un insieme di punti che definisce una forma nello spazio, caratterizzata da proprietà come lunghezza, area o volume, e può essere piana (2D) o solida (3D)

Le figure geometriche sono ovunque intorno a noi: dai cristalli di neve ai grattacieli, dai petali di un fiore alle costellazioni nel cielo. Ma cosa sono esattamente?

Una figura geometrica è una rappresentazione visiva o concettuale di forme definite da punti, linee, curve e superfici nello spazio.

Questi elementi semplici si combinano per creare strutture complesse, che sono alla base della matematica, dell'arte e persino della nostra percezione del mondo.

Figure piane e solide

Le figure geometriche si dividono principalmente in due categorie:

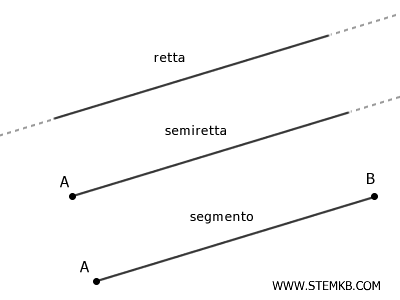
• Figure unidimensionali
  Le figure geometriche che si sviluppano in una sola dimensione, come punti, rette, semirette o segmenti, sono dette figure unidimensionali. Queste figure non hanno né larghezza né altezza, ma solo lunghezza (nel caso di rette o segmenti) o posizione nello spazio (nel caso di un punto). Sono le basi fondamentali della geometria, da cui si costruiscono le figure più complesse.
  
• Figure piane
  Le figure piane vivono in due dimensioni (2D), come quadrati, cerchi, triangoli e rettangoli. Le loro proprietà, come area e perimetro, possono essere calcolate con formule matematiche specifiche.
  

  Esempio. Un triangolo equilatero ha tutti i lati uguali e angoli di 60°. La sua simmetria lo rende un simbolo di armonia.

• Figure solide
  Le figure solide occupano tre dimensioni (3D), come cubi, sfere, piramidi e cilindri. Qui entrano in gioco concetti come volume e superficie.
  

  Esempio. Una sfera è la forma perfetta dal punto di vista geometrico, con ogni punto equidistante dal centro. È anche la forma naturale di molte strutture, come le bolle di sapone.

Le figure concave e convesse

Le figure concave e convesse si distinguono in base alla posizione del segmento che unisce due punti al loro interno:

• Figura convessa: Una figura è detta convessa se, per ogni coppia di punti \( A \) e \( B \) appartenenti alla figura, il segmento \( AB \) è interamente contenuto all'interno della figura.
  

  Esempio: Un cerchio, un rettangolo, o un triangolo sono figure convesse. Sono figure convesse anche le rette, le semirette e i segmenti. Per convenzione anche i punti sono considerati figure geometriche convesse.

• Figura concava: Una figura è detta concava se esiste almeno una coppia di punti \( A \) e \( B \) appartenenti alla figura tale che il segmento \( AB \) esca dalla figura stessa.
  
  

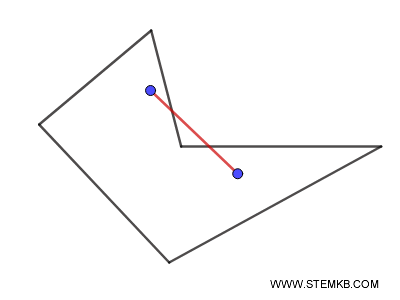
  Esempio: Una stella o un poligono con un angolo interno maggiore di 180° sono figure concave.

Questa classificazione è fondamentale in geometria perché influenza proprietà come il calcolo dell'area, le simmetrie e le applicazioni pratiche delle figure.

Quali sono le applicazioni delle figure geometriche?

Le figure geometriche trovano applicazione in numerosi ambiti: arte, architettura e ingegneria.

Da millenni l'uomo le utilizza per progettare edifici, ponti e strutture, utilizzando forme come triangoli (stabilità) e cerchi (efficienza strutturale).

Ad esempio, la pianta circolare del Pantheon a Roma o le piramidi di Giza sfruttano proprietà geometriche per stabilità ed estetica. Le travi triangolari sono fondamentali per la stabilità dei ponti, grazie alla loro capacità di distribuire uniformemente i carichi.

Nell'arte, le figure geometriche sono utilizzate per creare composizioni armoniose, prospettive realistiche e pattern visivi, spesso basandosi su proporzioni come il rapporto aureo.

Tuttavia, le figure geometriche sono molto più di semplici disegni su carta. Sono anche il linguaggio della natura, la chiave della tecnologia e l'essenza dell'arte.

Ad esempio, le celle esagonali di un alveare sono esagonali e sono un capolavoro della geometria naturale. Gli esagoni permettono di coprire una superficie senza lasciare spazi vuoti, minimizzando l’uso di cera e massimizzando la capacità di stoccaggio.

Quindi, studiare le figure geometriche non significa solo risolvere equazioni o tracciare linee, ma comprendere come l'universo stesso sia organizzato.

La prossima volta che noterai una forma intorno a te, fermati un momento e chiediti: quale figura geometrica si nasconde dietro? Potresti scoprire un mondo nuovo, pieno di ordine e meraviglia.