Il piano in geometria
Il piano è una delle entità fondamentali della geometria. E' qualcosa di molto semplice da immaginare ma immensamente utile.
Immagina un foglio di carta infinitamente esteso in tutte le direzioni. Questo foglio non ha spessore, è solo lunghezza e larghezza, un concetto puramente teorico.
Puoi considerare un piano anche come un insieme infinito di punti.
Qualsiasi punto che scegli su questo piano immaginario è parte del piano.
Se scegli due punti distinti a caso, puoi tracciare una linea retta che passa tra i punti e questa è sempre contenuta nel piano, senza mai uscirne.
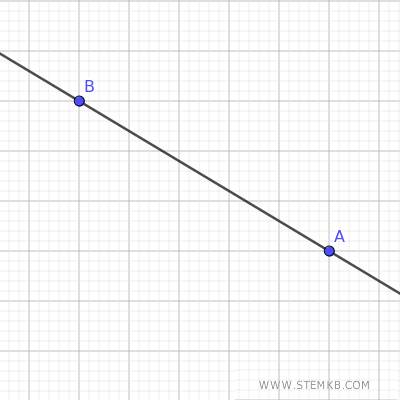
Se aggiungi un ulteriore punto al piano, puoi tracciare una seconda linea retta che interseca la precedente, formando un angolo.
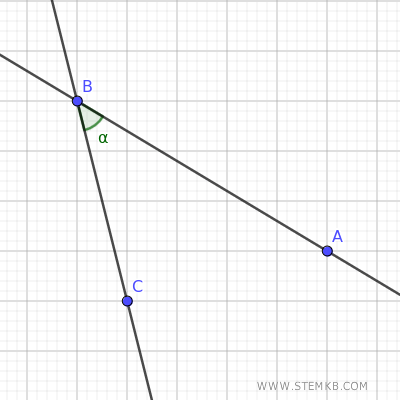
Aggiungendo un'altra linea retta definisci un triangolo, una delle più semplici figure geometriche
Il triangolo è la forma geometrica più semplice che si possa immaginare, perché è costituito da soli tre lati e tre angoli.
È la struttura di base da cui derivano tutti gli altri poligoni, una sorta di "mattone" fondamentale della geometria.
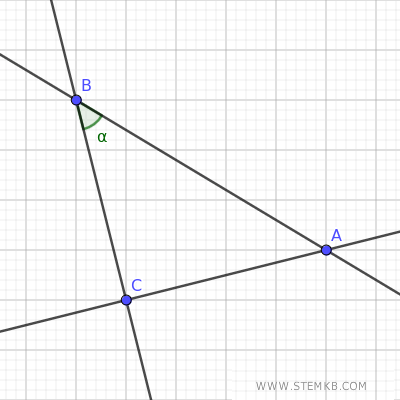
Il piano, quindi, è una base da cui partire per esplorare forme, angoli, e relazioni spaziali più complesse.
In geometria analitica, questo concetto si evolve con l'uso degli assi coordinati che ti permettono di esaminare relazioni tra diverse entità geometriche tramite il piano cartesiano.
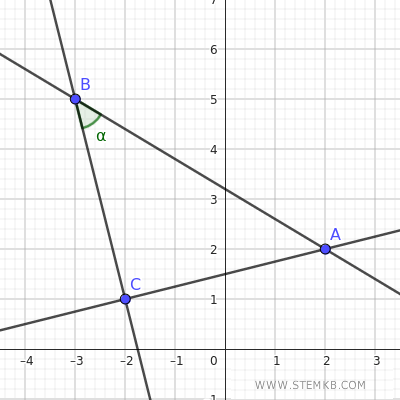
Inoltre, il piano non è solo un campo per tracciare linee e forme, ma è anche il luogo dove i concetti di parallelismo e perpendicolarità prendono vita.
Ad esempio, le linee rette parallele sul piano non si incontrano mai, indipendentemente da quanto vengono estese.
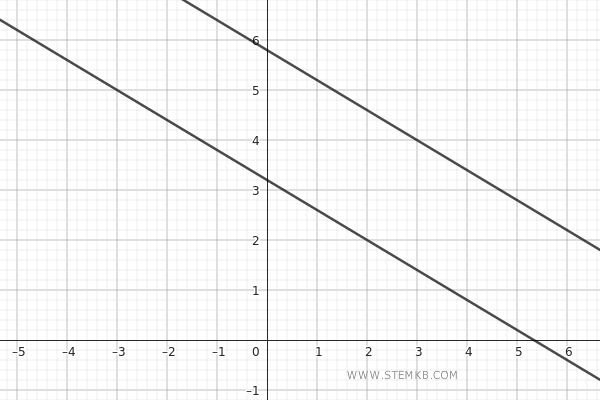
Le linee rette perpendicolari, invece, si intersecano formando angoli retti (90°), un concetto fondamentale per la comprensione di molte strutture geometriche.
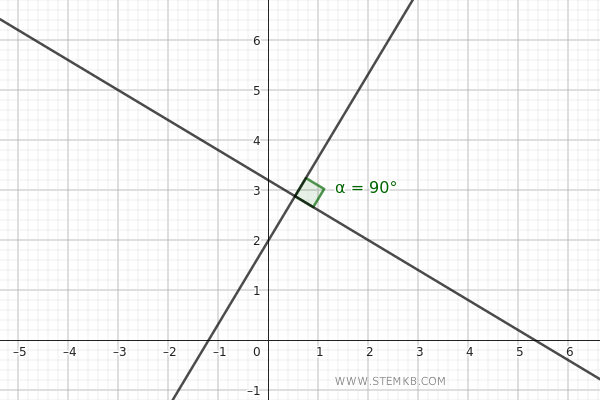
Queste relazioni elementari gettano le basi per concetti più complessi come le proprietà degli angoli, le simmetrie e le trasformazioni geometriche, rendendo il piano non solo una tela per disegnare, ma anche un laboratorio dove le leggi della geometria prendono forma e significato.
Gli assiomi del piano
Gli assiomi del piano nella geometria euclidea
- Ogni piano è un insieme di punti
Questo assioma stabilisce che un piano, nella geometria euclidea, è composto esclusivamente da punti. Ogni punto definisce una posizione nel piano, e non esistono entità aggiuntive oltre a questi punti. Quindi, un piano contiene un numero infinito di punti distribuiti uniformementeDa questo deduciamo che la geometria del piano si costruisce a partire dai punti. Grazie all'esistenza dei punti possiamo definire concetti come rette, segmenti, angoli, ecc.