Semiretta
Una semiretta è una parte di una retta che ha un punto di origine specifico e si estende indefinitamente in una sola direzione.
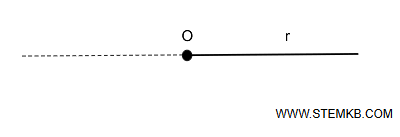
È definita a partire da un punto \( O \), chiamato origine o estremo, che divide la retta in due parti, e si considera solo una delle due.
I punti della semiretta diversi dall'origine sono detti punti interni della semiretta.
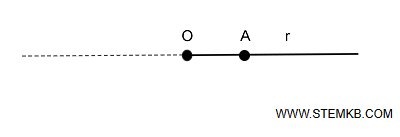
Una semiretta può essere indicata con una lettera minuscola, come le rette (es. r, s, ecc. ), oppure con la notazione \( \overrightarrow{OA} \), dove la prima lettera \( O \) rappresenta l'origine e la seconda \( A \) un punto qualsiasi che determina la direzione in cui la semiretta si estende.
L’idea della semiretta ci porta a riflettere sul concetto di infinito. Anche se la semiretta sembra "incompleta" perché manca di un’estremità, il suo prolungarsi indefinitamente in una direzione la distingue sia da un segmento (finito) sia da una retta (infinita in entrambe le direzioni).
Per fare un esempio pratico di semiretta, pensa a un raggio di luce che esce da una torcia: ha un punto di origine (la torcia stessa) e viaggia all'infinito in una direzione. Questo è un modo visivo di immaginare una semiretta.
Ogni retta può essere divisa in due semirette scegliendo un punto specifico della retta come origine \( O \).
Le due semirette così ottenute si estendono in direzioni opposte a partire da \( O \) e sono dette semirette opposte.
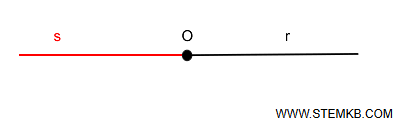
In altre parole, il sostegno di due semirette opposte è la retta che contiene sia l'origine \( O \) sia tutti i punti appartenenti a entrambe le semirette \( r \) e \( s \).
Ad esempio, considera una retta e un punto \( O \) su di essa.
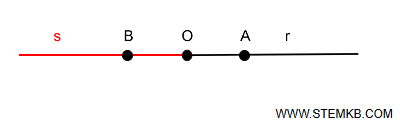
Le due semirette opposte \( r \) e \( s \) possono essere rappresentate come:
- \( \overrightarrow{OA} \), che si estende in una direzione;
- \( \overrightarrow{OB} \), che si estende nella direzione opposta.
Queste due semirette, pur avendo lo stesso punto di origine, non condividono alcun punto oltre \( O \), a meno che non vengano considerate insieme come la retta completa \( r \).
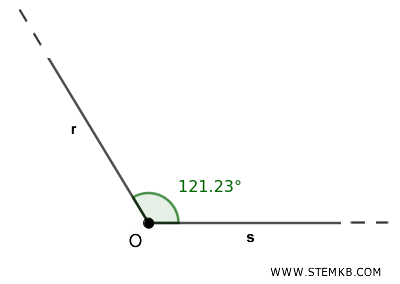
Le semirette hanno diverse applicazioni in geometria. Nella geometria elementare le semirette sono utilizzate per definire angoli. Ad esempio, un angolo è infatti formato da due semirette \( r \) e \( s \) che condividono la stessa origine \( O \).