La congruenza in geometria
Cos'è la congruenza?
Due figure geometriche A e B, come segmenti o angoli, sono congruenti quando sono esattamente uguali in forma e dimensione, indipendentemente dalla loro posizione o dal loro orientamento nello spazio. $$ A \cong B $$
La congruenza è un principio che ti aiuta a stabilire l'uguaglianza di forma e dimensione tra elementi geometrici.
In altre parole, due figure sono congruenti quando le puoi sovrapporle l'una sopra l'altra, facendo coincidere tutti i loro punti, dopo uno spostamento, una rotazione o una riflessione.
E' un concetto che puoi applicare alle figure geometriche complesse come i poligoni, ma anche a elementi più semplici come segmenti e angoli. Esploriamo questi concetti in dettaglio:
Segmenti congruenti
La congruenza tra segmenti di linea si verifica quando due segmenti hanno esattamente la stessa lunghezza.
Non importa se i segmenti sono orientati in modo diverso o si trovano in posizioni diverse nello spazio. Se la loro lunghezza è la stessa, sono congruenti.
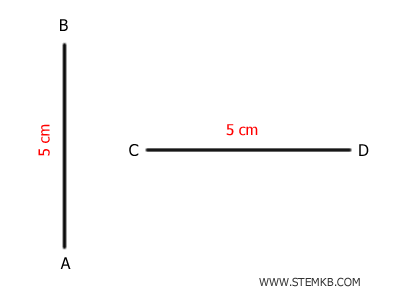
Ad esempio, se hai due segmenti, uno disegnato verticalmente (AB) e l'altro orizzontalmente (CD), e entrambi misurano esattamente 5 cm, allora puoi affermare che sono segmenti congruenti $ \overline{AB} \cong \overline{CD} $.
Angoli congruenti
Due angoli sono congruenti quando hanno la stessa ampiezza.
L'orientamento degli angoli o la lunghezza dei loro lati non influisce sulla loro congruenza.
Per esempio, se due angoli α e β misurano entrambi 30 gradi, sono angoli congruenti $ \alpha \cong \beta $ , indipendentemente da dove si trovano o da come sono disegnati.
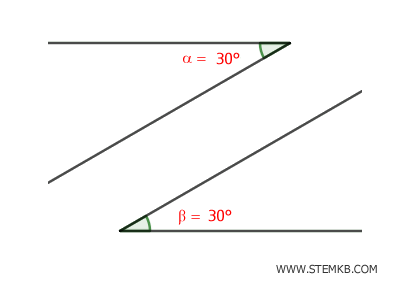
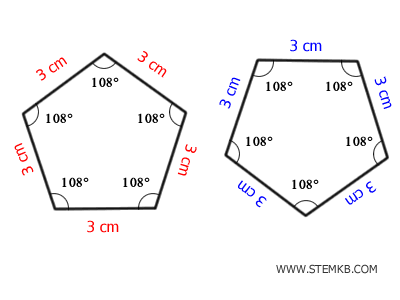
Figure geometriche congruenti
Le figure geometriche sono congruenti quando corrispondono esattamente in termini di forma e dimensione.
Questo si applica a qualsiasi tipo di figura: triangoli, quadrati, rettangoli, cerchi, ecc.
Per dimostrare che due figure sono congruenti, deve mostrare che tutti i loro corrispondenti lati e angoli sono congruenti.
Ad esempio, due poligoni regolari (ad esempio, due pentagoni regolari) sono congruenti se i loro corrispondenti lati e angoli interni sono congruenti. Se un pentagono regolare ha tutti i lati di 3 cm e un altro pentagono regolare ha anche tutti i lati di 3 cm, allora sono congruenti.

Nel caso del triangolo esistono anche dei criteri rapidi per verificare la congruenza che puoi utilizzare quando non hai tutte le informazioni sulla lunghezza dei lati e l'ampiezza degli angoli.
Per esempio, nel criterio Lato-Lato-Lato (LLL), se i tre lati di un triangolo sono congruenti ai tre lati di un altro, i triangoli sono congruenti. Nel criterio Lato-Angolo-Lato (LAL) ti basta conoscere la lunghezza di due lati e dell'angolo tra di essi. Infine, nel criterio Angolo-Lato-Angolo (ALA) solo la lunghezza di un lato e degli angoli adiacenti. Sono criteri speciali che si applicano solo ai triangoli.
Anche oggetti tridimensionali possono essere congruenti.
Ad esempio, due sfere di uguale raggio, due cubi con spigoli della stessa lunghezza, o due cilindri con la stessa altezza e raggio di base sono esempi di figure tridimensionali congruenti.