Poligoni

Un poligono è una figura geometrica piana delimitata da una poligonale chiusa e non intrecciata.

La poligonale rappresenta la "frontiera" o il "contorno" del poligono e delimita uno spazio interno che fa parte della figura.

I segmenti che compongono la poligonale si chiamano lati del poligono, mentre i punti in cui questi segmenti si incontrano prendono il nome di vertici.

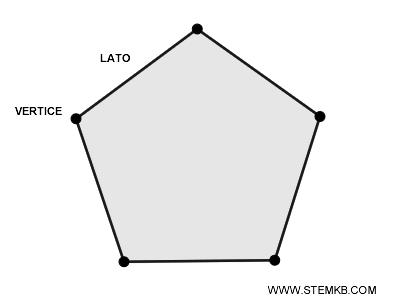
È quindi possibile immaginare un poligono come una sorta di recinto geometrico che separa ciò che è "dentro" da ciò che è "fuori".

Il poligono include sia il contorno della poligonale (detto anche "frontiera") sia i punti interni rispetto alla poligonale.

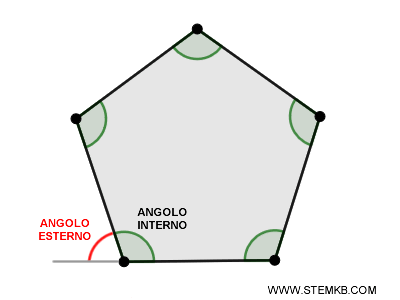
Un altro elemento dei poligoni, oltre i lati e i vertici, sono gli angoli che possono essere interni o esterni.

• Angolo interno. E' un angolo convesso individuato da due lati consecutivi del poligono che ha per origine il vertice in comune ai due lati.
• Angolo esterno. E' un angolo adiacente all'angolo interno

Un fatto curioso e utile riguarda la somma degli angoli interni di un poligono. Se un poligono ha \( n \) lati, la somma degli angoli interni è data dalla formula:

$$ \text{Somma angoli interni} = 180^\circ \times (n - 2) $$

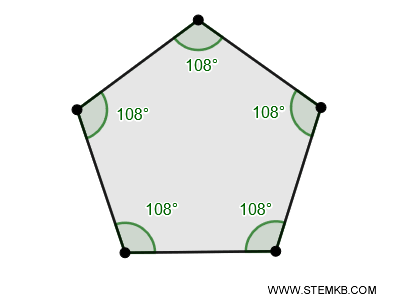
Ad esempio, in un triangolo (\( n = 3 \)) la somma degli angoli interni è sempre \( 180^\circ \times 1 = 180^\circ \), in un quadrilatero (\( n = 4 \)) la somma è \( 180^\circ \times 2 = 360^\circ \), mentre in un pentagono (\( n = 5 \)) la somma è \( 180^\circ \times 3 = 540^\circ \).

Altri elementi tipici di un poligono sono le diagonali e le corde.

Quando parliamo di diagonale del poligono intendiamo un segmento che ha per estremi due vertici distinti e non consecutivi del poligono, passando all’interno della figura.

Ad esempio, in un pentagono, ogni vertice può essere collegato con altri tre vertici tramite diagonali.

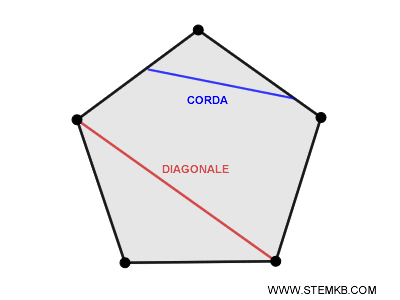
Si parla di corda, invece, per intendere un qualsiasi segmento che congiunge due punti del contorno appartenenti a lati diversi del poligono.

I poligoni si classificano in base a diversi criteri, tra cui:

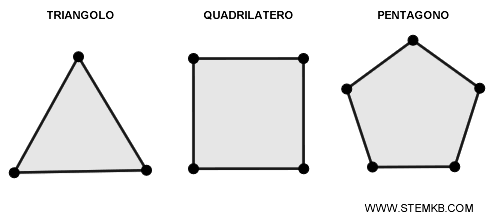
• Numero di lati o angoli: un triangolo ha tre lati/angoli, un quadrilatero ne ha quattro, un pentagono cinque, un esagono ne ha sei e così via.
  
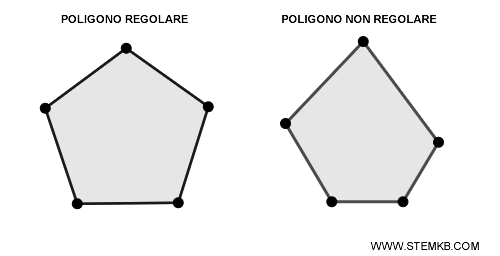
• Regolarità: un poligono è regolare se ha tutti i lati e gli angoli uguali; altrimenti è irregolare. Nei poligoni regolari, oltre ad avere lati e angoli congruenti, esiste un punto chiamato centro che è equidistante da tutti i vertici.
  
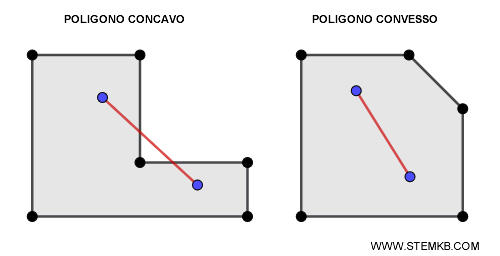
• Convessità: un poligono è convesso se tutti i segmenti che congiungono due punti qualsiasi del poligono si trovano interamente all’interno della figura; altrimenti è concavo.
  

In conclusione, il poligono rappresenta uno dei concetti fondamentali della geometria. Con un po' di attenzione possiamo scorgere un poligono negli oggetti che ci circondano, scoprendo la geometria nascosta dietro ogni forma.