Enti geometrici fondamentali

Gli enti geometrici fondamentali (o primitivi) sono entità per le quali non viene data nessuna definizione. Costituiscono la base della geometria e vengono accettati come veri senza dimostrazione. 

Questi enti sono considerati assiomi, ovvero proposizioni che si assumono vere a priori per costruire una teoria.

Non si definiscono formalmente perché sono concetti intuitivi che si assumono come base del ragionamento geometrico.

La loro esistenza e le proprietà sono accettate senza bisogno di dimostrazione, permettendo così di sviluppare ulteriori teorie e dimostrazioni.

Nella geometria, gli enti fondamentali sono i punti, le rette e i piani.

• Punti
  Un punto rappresenta una posizione nello spazio e non ha dimensioni. È l'elemento più semplice della geometria. Ad esempio, puoi pensare ai punti come alle coordinate su una mappa che identificano specifiche località. In genere sono indicati con le lettere maiuscole dell'alfabeto (es. A, B, C, ...).
  
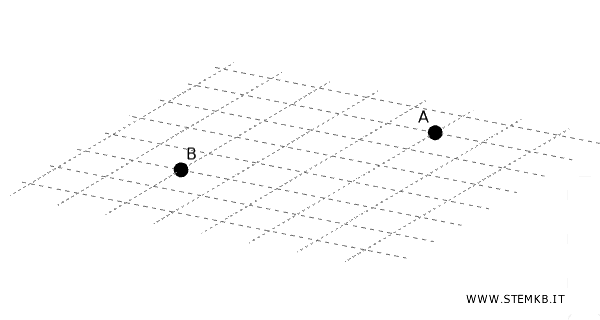
• Rette
  Una retta è una successione infinita di punti allineati nella stessa direzione. È infinita in entrambe le direzioni e non ha spessore. Ad esempio, puoi immaginare una retta come la traiettoria di un raggio di luce che si estende all'infinito. In genere sono indicati con le lettere minuscole dell'alfabeto (es. r, s, t, ...).
  
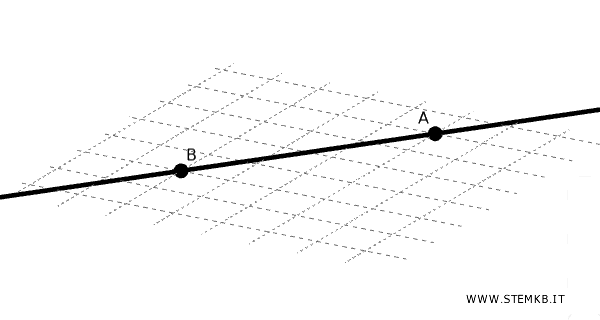
• Piani
  Un piano è una superficie bidimensionale infinita, costituita da una successione di rette. Un esempio pratico di piano è la superficie di una lavagna infinita, senza bordi.  In genere sono indicati con le lettere minuscole dell'alfabeto greco (es. α, β, γ, ...).
  

Gli enti primitivi, come i punti, le rette e i piani, costituiscono la base per definire e costruire tutte le altre figure geometriche più complesse, che non sono enti primitivi. Ad esempio, triangoli, poligoni, ecc.

Esempi Pratici

Esempio 1

Ad esempio, per costruire un triangolo, iniziamo con tre punti non allineati (A, B e C). Poi, tracciamo le rette che li collegano, formando così il triangolo.

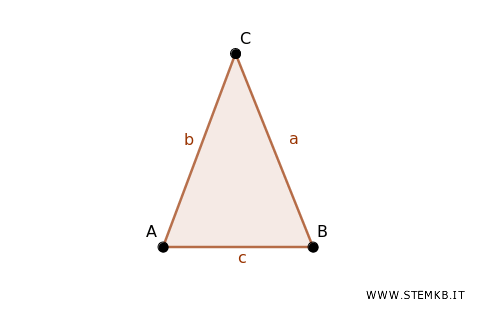
Qui, i punti e le rette sono utilizzati come enti geometrici fondamentali.

Esempio 2

Immaginiamo due fogli di carta infiniti (piani) che si intersecano. La linea dove si incontrano è una retta.

Qui, i piani e la retta d'intersezione sono considerati enti geometrici.

Esempio 3

In un sistema di coordinate, ogni punto può essere descritto da un insieme di coordinate (x, y).

Le rette sono le linee che seguono le direzioni delle coordinate, e il piano XY, ad esempio, è la superficie su cui vengono tracciati questi punti e rette.

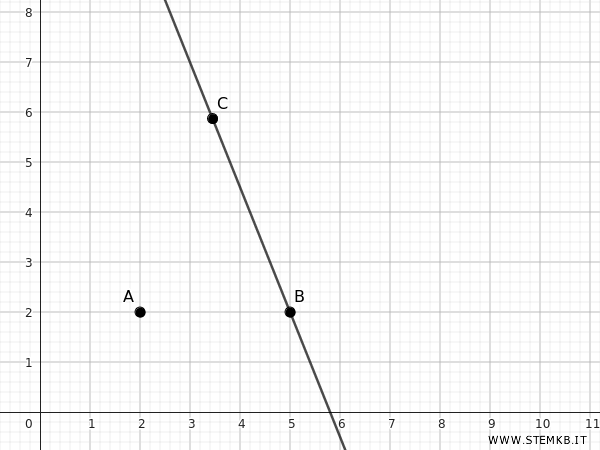
Questi esempi dimostrano come gli enti geometrici fondamentali formano la base per costruire e comprendere figure più complesse nella geometria.

Sono i mattoni senza i quali la struttura della geometria non potrebbe esistere.