Gli angoli in geometria

Gli angoli sono dappertutto: nell'apertura di una porta, nella forma di un tetto, e anche nel piegare un foglio di carta. Capirli ci aiuta a comprendere meglio il mondo intorno a noi.

Cos'è un angolo?

Un angolo si forma quando due semirette hanno la stessa orgine, un punto noto come vertice.

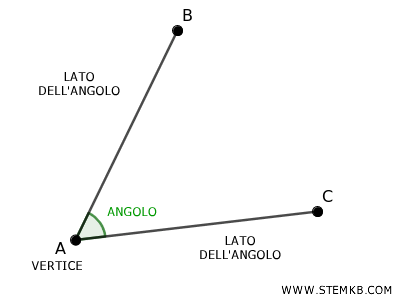
Le semirette, chiamate lati dell'angolo, si estendono indefinitamente da questo punto di incontro.

L'angolo è una delle parti in cui il piano viene diviso dalle semirette.

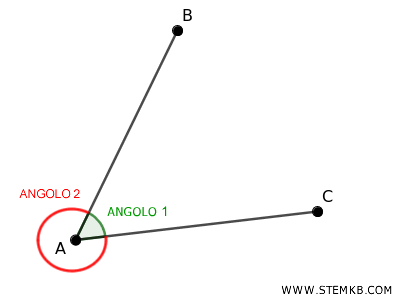
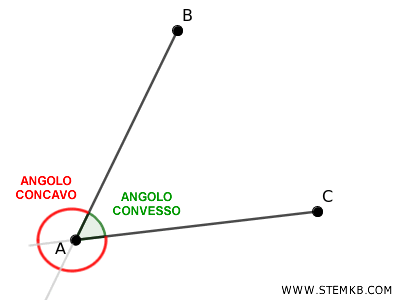
A parte che il caso particolare di un angolo piatto, uno dei due angoli è concavo e l'altro angolo è convesso.

Un angolo è concavo se la sua ampiezza è maggiore di 180°, e la parte interna include il prolungamento dei lati. Un angolo è convesso se la sua ampiezza è minore o uguale a 180° e non include il prolungamento dei lati.

In altre parole, l'angolo è la misura della rotazione necessaria per spostare un lato verso l'altro.

Generalmente viene misurato in senso antiorario.

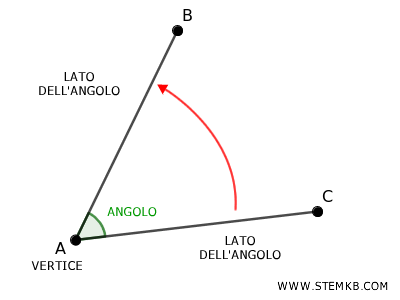
In parole più semplici, misura di quanto devi ruotare un lato dell'angolo per sovrapporlo all'altro.

Ad esempio, immagina di aprire un libro aperto sul tavolo. Il punto in cui le due pagine si incontrano è come il vertice di un angolo, e i bordi delle pagine sono i lati. L'angolo è lo spazio tra queste "pagine", ovvero tra i lati. Per chiudere il libro devi portare un lato del libro sull'altro.

Come si indica un angolo?

Esistono diverse notazioni per rappresentare un angolo.

Si può indicare l'angolo come \( AÔB \), dove \( A \) e \( B \) sono punti appartenenti ai lati dell'angolo.

In alternativa, è possibile utilizzare il simbolo \( \angle AÔB \).

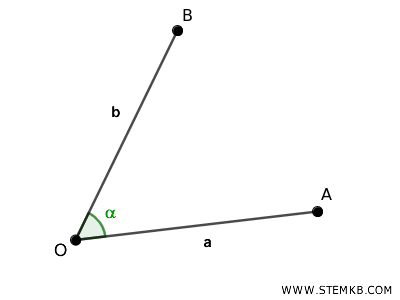
L'angolo può essere espresso anche facendo riferimento alle semirette \( a \) e \( b \) che costituiscono i suoi lati, mediante la notazione \( aÔb \).

Una scrittura più sintetica è \( ab \), che specifica solo i due lati dell'angolo, senza indicarne il vertice.

È possibile rappresentare l'angolo anche con \( Ĉ \), specificando esclusivamente il vertice, senza precisare i lati.

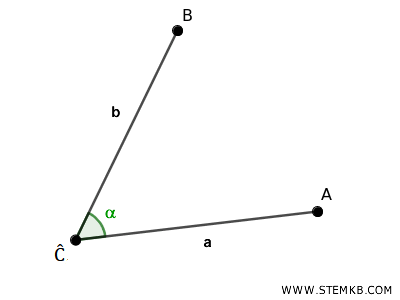
Spesso, per comodità, si assegnano agli angoli lettere minuscole dell'alfabeto greco, come \( \alpha \), \( \beta \), \( \gamma \), ecc.

Queste sono le principali modalità alternative per indicare un angolo.

Come misuriamo gli angoli?

Per misurare l'ampiezza di un angolo, devi usare strumenti come il goniometro, uno strumento semicircolare o circolare graduato. E' essenziale nel disegno tecnico.

Puoi misurare un angolo tramite diverse unità di misura: in gradi, radianti o giri.

• Gradi
  Un grado corrisponde a 1/360 di un giro completo in una circonferenza o in cerchio. Quindi, per fare un giro completo sono necessari 360°. Per fare mezzo giro, 180°, ecc. Questa unità di misura degli angoli risale addirittura agli antichi babilonesi che dividevano un cerchio in 360 parti.

  Ad esempio, immagina un cerchio come quello di un orologio diviso in 360 parti anziché 60 minuti.

• Radianti
  Un radiante è l'angolo che determina un arco di circonferenza con la stessa lunghezza del raggio.
• Giri
  Un giro rappresenta un angolo che completa un cerchio intero. Corrisponde a 360° gradi e a 2π radianti.

Una volta capito come si misurano gli angoli, possiamo vedere quali tipi di angoli esistono.

Tipi di angoli

Esistono diversi tipi di angoli a seconda della loro ampiezza:

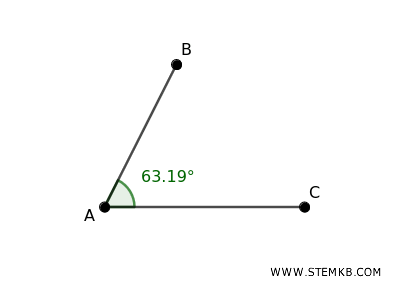
• Angoli acuti
  Sono gli angoli più piccoli, quelli con un'ampiezza inferiore a 90 gradi, come l'angolo formato da una fetta di pizza.
  
• Angoli retti
  Sono angoli che hanno un'ampiezza esattamente di 90 gradi, come l'angolo di un foglio di carta. Le linee che formano un angolo retto sono dette perpendicolari.
  
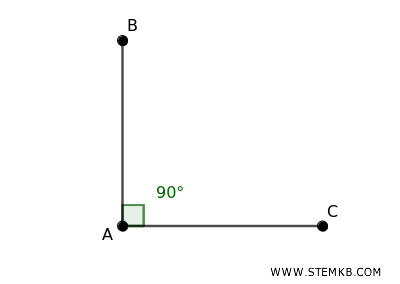
• Angoli ottusi
  Sono più grandi di un angolo retto ma meno di un angolo piatto, come l'angolo formato da due braccia aperte meno che completamente.
  
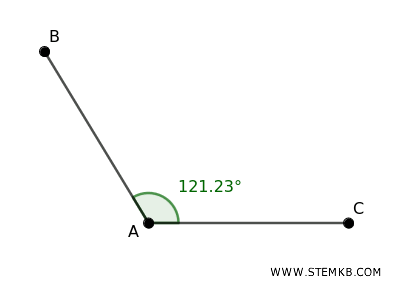
• Angoli piatti
  Hanno un'ampiezza di 180 gradi. I due lati dell'angolo sono opposti e formano una linea retta. E' l'angolo che formi quando apri le braccia in direzioni opposte.
  
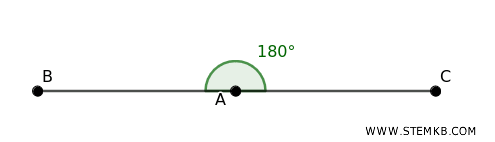
• Angolo giro
  Un angolo giro ha un'ampiezza di 360°. Si chiama così perché compie un giro completo del cerchio. Ad esempio, se giri completamente su te stesso, fai un giro di 360 gradi, che è anche la misura di un angolo giro. In questo caso i due lati sono coincidenti.
  
• Angolo nullo
  Un angolo nullo è ogni angolo che ha i lati coincidenti e, a differenza dell'angolo giro, non contiene altri punti oltre quelli dei suoi lati.
  

Le relazioni tra gli angoli

Tra due angoli che condividono lo stesso vertice possono nascere diverse relazioni.

• Angoli consecutivi
  Due angoli consecutivi condividono un lato, mentre gli altri lati si estendono in direzioni opposte, ma partendo dallo stesso punto.
  
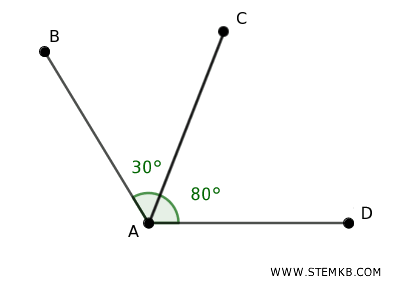
• Angoli adiacenti
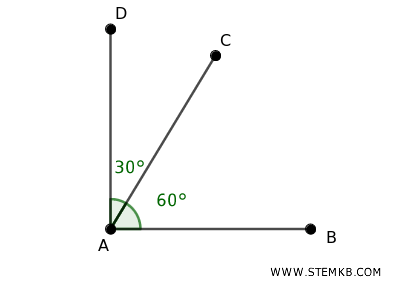
  Questi angoli si trovano fianco a fianco, condividendo sia un lato sia un vertice. La loro somma è pari a 180 gradi, formando una linea retta. Quindi sono angoli consecutivi particolari, con una somma congruente a un angolo piatto.
  
• Angoli complementari
  Sono coppie di angoli che, sommati, danno un angolo retto di 90 gradi. Indipendentemente dalle loro dimensioni individuali, la loro combinazione crea sempre un angolo perfettamente retto. Non necessariamente hanno un angolo e un vertice in comune.
  
• Angoli supplementari
  Non sono necessariamente adiacenti ma la somma di questi angoli è sempre 180 gradi.
  

  Quale differenza c'è tra gli angoli adiacenti e gli angoli supplementari? Gli angoli adiacenti sono sempre vicini e condividono un vertice e un lato, formando insieme un angolo piatto di 180 gradi. Gli angoli supplementari, invece, non devono necessariamente essere adiacenti o condividere un lato o un vertice; la loro caratteristica principale è che la somma dei loro angoli equivale a 180 gradi, indipendentemente dalla loro posizione reciproca.

• Angoli esplementari
  Due angoli sono esplementari se la loro somma è un angolo giro, ossia 360 gradi.
  
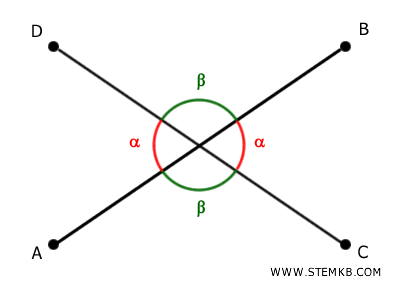
• Angoli opposti al vertice
  Si formano quando due linee rette si incrociano, generando due coppie di angoli opposti. Sono uguali in ampiezza (congruenti) e mantengono una simmetria perfetta. I prolungamenti dei lati di un angolo sono i lati di un altro angolo.
  

Gli angoli non sono solo una parte della matematica, ma un aspetto fondamentale del modo in cui vediamo e interagiamo con il mondo. Sono ovunque e in tutto ciò che facciamo.

Gli angoli trovano applicazioni pratiche in numerosi campi. In architettura e ingegneria, la comprensione degli angoli è essenziale per la progettazione e la costruzione di edifici e strutture. In astronomia, gli angoli aiutano a calcolare posizioni e traiettorie di corpi celesti, ecc.