Il baricentro di un triangolo
Il baricentro di un triangolo è il punto in cui si incontrano le tre mediane del triangolo, quelle linee che congiungono ciascun vertice con il punto medio del lato opposto.
Per immaginarlo, pensa a un triangolo di qualsiasi forma e dimensione: isoscele, equilatero o scaleno.
Ogni mediana divide il triangolo in due parti di uguale area.
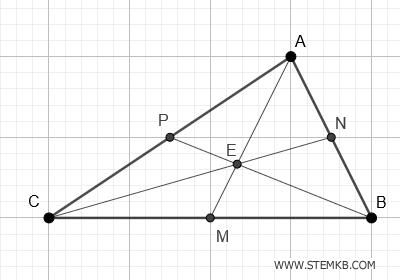
Il punto di incontro di queste mediane (E) è il baricentro. E' come il centro di gravità del triangolo.
Un aspetto interessante del baricentro è la sua posizione sempre all'interno del triangolo, indipendentemente dalla sua forma.
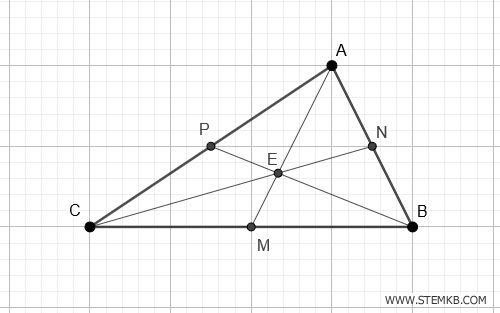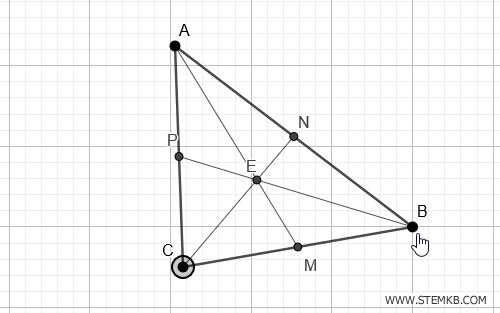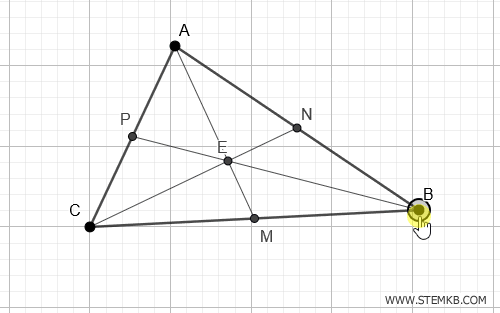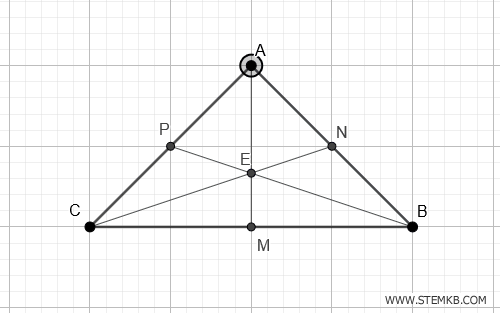
Inoltre, il baricentro si trova esattamente a due terzi della distanza da ciascun vertice lungo la mediana corrispondente.
Questo significa che il baricentro divide ogni mediana in una proporzione di 2:1, con la parte più lunga che si estende dal vertice al baricentro.
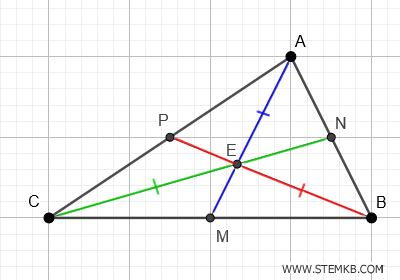
Ad esempio, il segmento EB è congruente con il doppio del segmento EP. E così anche gli altri.
$$ \overline{EB} \cong 2 \cdot \overline{EP} $$
$$ \overline{EA} \cong 2 \cdot \overline{EM} $$
$$ \overline{EC} \cong 2 \cdot \overline{EN} $$
Nel caso di un triangolo equilatero, il baricentro si trova anche al centro geometrico del triangolo.
In questo caso il baricentro coincide con l'ortocentro, il circocentro e l'incentro.
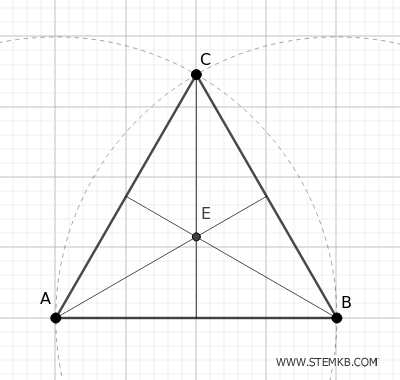
Nelle altre forme del triangolo, invece, la sua posizione varia in base alle proporzioni e angoli del triangolo.
Il baricentro, è un concetto fondamentale non solo in geometria, ma anche in diverse applicazioni pratiche come l'ingegneria e la fisica, dove il bilanciamento e la distribuzione della massa sono elementi cruciali.
Ad esempio, da un punto di vista pratico, il baricentro può essere utilizzato per trovare il centro di gravità di una lamina sottile a forma di triangolo. Se poggi il triangolo su un supporto, posizionandolo esattamente sotto il baricentro, il triangolo rimane in equilibrio, dimostrando così che il baricentro è il punto in cui la massa del triangolo è perfettamente bilanciata.
Per calcolare il baricentro, puoi utilizzare le formule matematiche o, in modo più intuitivo, tracciare le mediane del triangolo e trovare il loro punto di intersezione come ti ho già spiegato.