Il semipiano
Cos'è un semipiano?
Un semipiano è una figura geometrica ottenuta dividendo un piano attraverso una retta.
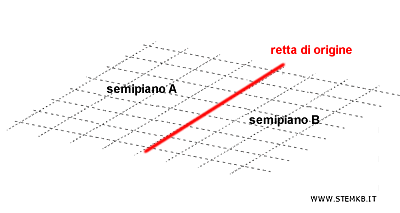
Ogni retta del piano separa quest'ultimo in due semipiani opposti.
Immagina una superficie piatta infinita, come un foglio di carta che si estende all'infinito in ogni direzione.
Tracciando una linea retta, questa suddivide il piano in due regioni distinte. Ognuna di queste due parti è un semipiano, e la retta che le separa prende il nome di origine o frontiera del semipiano.
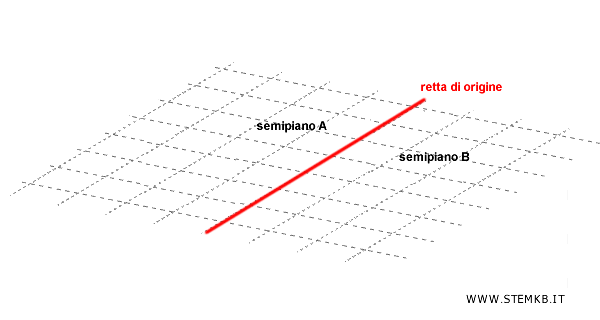
Nota che la retta di origine appartiene ad entrambi i semipiani.
I punti interni a un semipiano, invece, sono quelli che si trovano esclusivamente in una delle due porzioni di piano, senza toccare la retta di origine.
Questa distinzione è fondamentale perché la retta agisce come un confine: i punti "interni" a un semipiano non possono essere confusi con quelli che appartengono alla frontiera.
Per rendere l'idea più tangibile, immaginae di stare davanti a una porta aperta. La porta stessa è la retta di origine. I due ambienti che la porta separa — ad esempio, il salotto e un'altra stanza — rappresentano i due semipiani opposti. Ogni punto del salotto appartiene al semipiano interno corrispondente, così come ogni punto del corridoio appartiene all'altro semipiano. La soglia della porta, invece, è la frontiera comune a entrambi.

Pur essendo un concetto semplice, il semipiano ci permette di analizzare lo spazio in maniera più ordinata.
Assioma di partizione del piano mediante una retta
Una retta \( r \) in un piano suddivide l'insieme dei punti del piano in due sottoinsiemi disgiunti e convessi, denominati \( \alpha \) e \( \beta \).
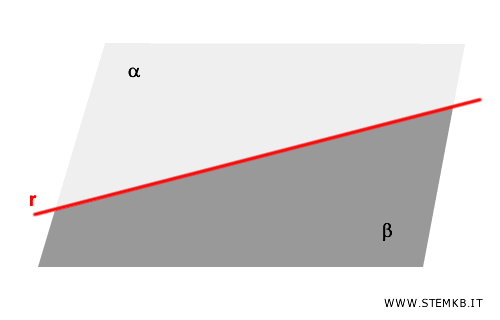
La proprietà fondamentale di questa partizione è che, preso un punto \( A \) appartenente a \( \alpha \) e un punto \( B \) appartenente a \( \beta \), il segmento \( AB \) interseca la retta \( r \) in un unico punto.

Questo assioma è utile per descrivere in modo rigoroso come una retta suddivide il piano in due regioni ben definite, dette semipiani.
L'assioma introduce anche il concetto di convessità, una proprietà fondamentale in molte aree della matematica.
I due sottoinsiemi generati da una retta sono convessi, il che significa che il segmento che unisce due punti interni a uno stesso semipiano rimane interamente all'interno del semipiano.