Introduzione ai triangoli in geometria

Un triangolo è un poligono formato da tre lati e tre angoli, può sembrare una figura geometrica elementare, ma è ricco di proprietà molto importanti nello studio della geometria.

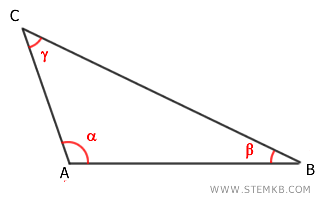
Ogni vertice del triangolo è l'intersezione di due lati e ogni lato è compreso tra due vertici.

Ad esempio, il vertice A è compreso tra i lati AB e AC.

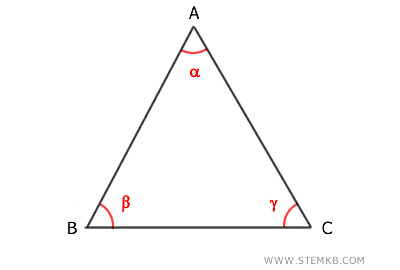
Ogni lato del triangolo è adiacente a due angoli ed è opposto al terzo angolo.

Ad esempio, il lato AB è adiacente agli angoli α e β ed è il lato opposto all'angolo γ.

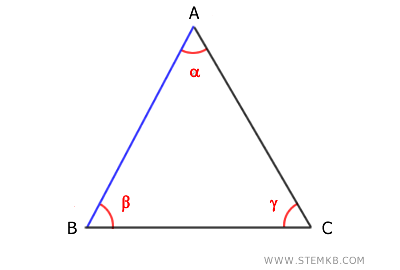
Allo stesso modo ogni angolo è adiacente a due lati del triangolo ed è opposto al terzo lato. Ad esempio, l'angolo γ è adiacente ai lati AC e BC ed è l'angolo opposto al lato AB.

La classificazione dei triangoli

Partiamo dalla classificazione dei triangoli. In base agli angoli, abbiamo tre tipi di triangoli

• I triangoli acutangoli hanno tutti gli angoli acuto ossia con un ampiezza minore di 90 gradi.
  
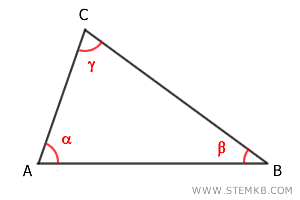
• I triangoli rettangoli hanno un angolo retto, esattamente di 90 gradi.
  
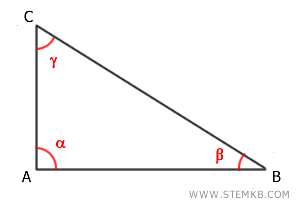
• I triangoli ottusangoli hanno un angolo ottuso, superiore a 90 gradi.
  

Questa distinzione ti aiuterà a capire come si comportano i triangoli in diverse situazioni.

Per esempio, prendi un triangolo rettangolo. Qui entra in gioco il famoso teorema di Pitagora che è applicabile solo ai triangoli rettangoli. Il teorema di Pitagora afferma che in un triangolo rettangolo, la somma delle aree dei quadrati costruiti sui cateti (i lati più corti) è uguale all'area del quadrato costruito sull'ipotenusa (il lato più lungo). Questo teorema ha un'enorme importanza in matematica e ingegneria. Pensa a come viene utilizzato per calcolare distanze in situazioni reali, come in architettura o nella navigazione.

Un altro aspetto interessante dei triangoli è la loro classificazione in base ai lati:

• I triangoli equilateri hanno tutti i lati uguali (congruenti).
  
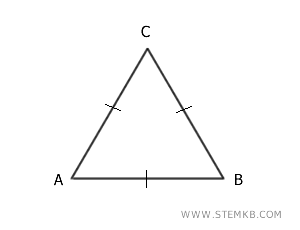
• I triangoli isosceli hanno due lati uguali (congruenti).
  
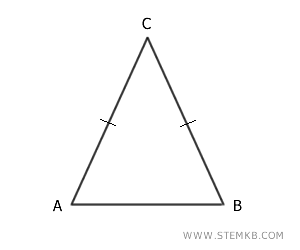
• I triangoli scaleni non hanno nessun lato uguale.
  

Anche in questo caso ogni tipo di triangolo ha le sue peculiarità.

Ad esempio, in un triangolo equilatero, tutti gli angoli sono uguali e misurano 60 gradi. Questa simmetria diventa molto utile quando devi calcolare l'area, l'altezza o il perimetro.

I segmenti notevoli del triangolo

I segmenti notevoli di un triangolo sono particolari segmenti di riferimento che vengono utilizzati in geometria per studiare le proprietà e le caratteristiche del triangolo.

Ecco i principali segmenti notevoli del triangolo:

• Bisettrice: È il segmento che divide un angolo interno del triangolo in due parti uguali, partendo dal vertice dell'angolo e terminando sul lato opposto. La bisettrice è sempre interna al triangolo e il punto in cui le tre bisettrici interne si incontrano è detto incentro, centro della circonferenza inscritta nel triangolo.
  
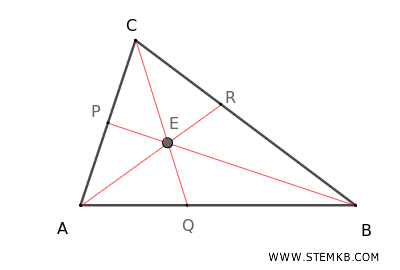
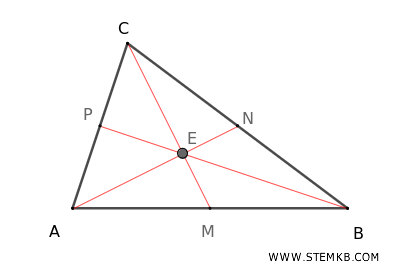
• Mediana: È il segmento che congiunge un vertice del triangolo con il punto medio del lato opposto. Ogni triangolo ha tre mediane (AN, BP, CM), una per ogni lato, e il loro punto di incontro (E) è detto baricentro, che rappresenta il centro di massa del triangolo.
  
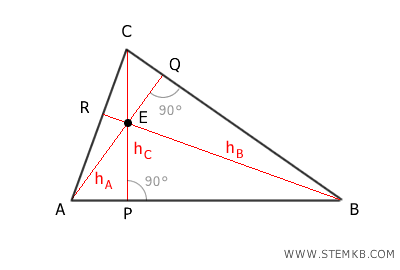
• Altezza: È il segmento perpendicolare condotto da un vertice al lato opposto (o al suo prolungamento). L'altezza può essere interna o esterna al triangolo, a seconda del tipo di triangolo considerato. Il punto di intersezione delle tre altezze è detto ortocentro.
  

Questi segmenti sono fondamentali nello studio della geometria euclidea e delle proprietà dei triangoli, poiché definiscono dei punti notevoli molto importanti (es. baricentro, incentro, ortocentro, circocentro) e ti permettono di stabilire delle relazioni geometriche utili alla risoluzione di problemi.

Le proprietà dei triangoli

Una proprietà universale dei triangoli è la somma degli angoli interni di un triangolo, che è sempre di 180 gradi.

Non importa che tipo di triangolo sia, scaleno o equilatero, acutangolo, rettangolo o ottusangolo... la somma degli angoli interni è sempre uguale a un angolo piatto ossia a 180°.

Questa regola ti offre un metodo per calcolare l'angolo mancante in un triangolo se conosci già gli altri due. È un principio fondamentale dei triangoli da non dimenticare mai.

Un'altra proprietà interessante dei triangoli è il teorema dell'angolo esterno, secondo il quale l'angolo esterno di un triangolo è sempre uguale alla somma degli angoli interni non adiacenti.

Questo teorema ti aiuta a comprendere meglio le relazioni tra gli angoli in un triangolo.

In geometria, i triangoli sono anche la base per la definizione di altre figure geometriche, come poligoni e poliedri. Ad esempio, un poligono può essere suddiviso in triangoli, e la somma degli angoli interni di un poligono è un multiplo di 180 gradi, un concetto che deriva direttamente dalle proprietà dei triangoli.

Inoltre, i triangoli sono fondamentali in trigonometria, una branca della matematica che esplora le relazioni tra lati e angoli nei triangoli. Questo studio ha applicazioni pratiche in vari campi, dalla fisica all'ingegneria. Ma forse è troppo presto per parlartene.

In conclusione, i triangoli non sono solo una figura geometrica semplice, ma una struttura fondamentale in molti campi della scienza e della tecnologia.