La mediana
La mediana è un segmento che parte da un vertice di un triangolo e si dirige esattamente verso il punto medio del lato opposto.
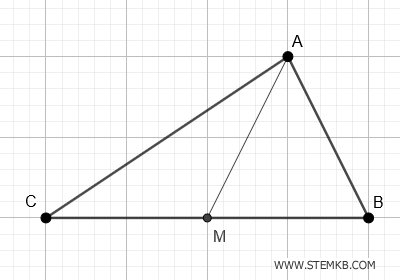
Questa linea, che può sembrare banale a prima vista, in realtà cela una profonda verità geometrica.
Prendi, ad esempio, un triangolo qualunque, chiamalo ABC.
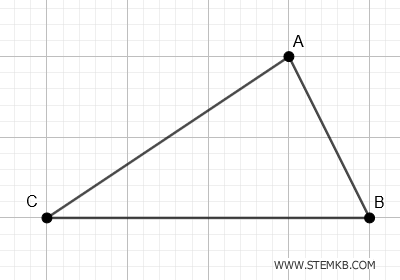
La mediana che parte dal vertice A scende in modo deciso e inequivocabile verso il punto medio del lato BC.
Il punto medio del lato BC è il punto M che divide questo segmento a metà ed è equidistante dagli estremi B e C.
Quindi, una mediana del triangolo è il segmento AM.

Questa non è solo una divisione fisica del triangolo, ma anche una sorta di ponte tra angoli e lati, che ti aiuta a comprendere meglio la sua struttura.
Ma questa è solo una mediana del triangolo... ce ne sono altre.
Quante mediane ci sono in un triangolo?
Ogni triangolo ha tre mediane, una per ogni vertice e lato.
Ad esempio, trova il punto medio N del segmento AB. Poi traccia un segmento dal punto medio N al vertice C del triangolo.
Il segmento AN è un'altra mediana del triangolo.
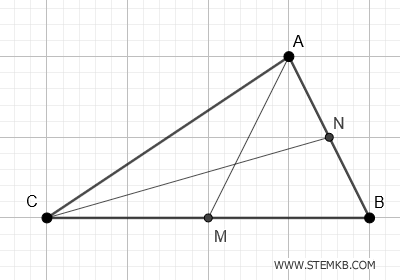
Allo stesso modo puoi disegnare l'ultima mediana BP, quella che collega l'estremo B al punto medio P del lato AC del triangolo.
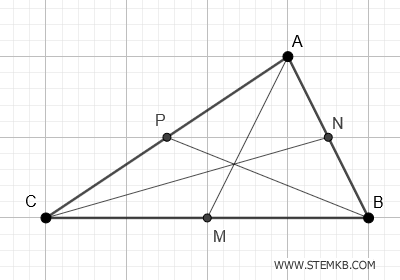
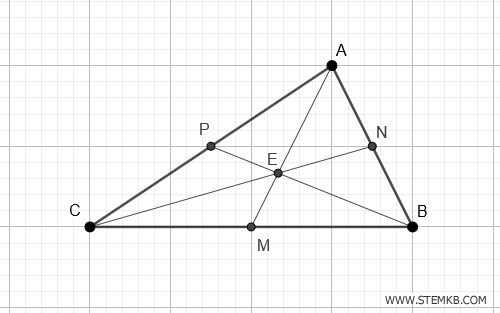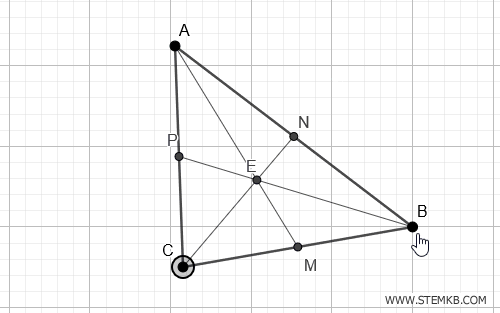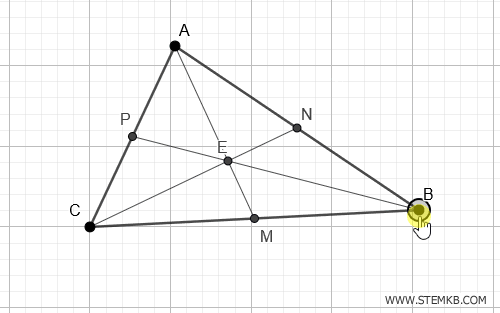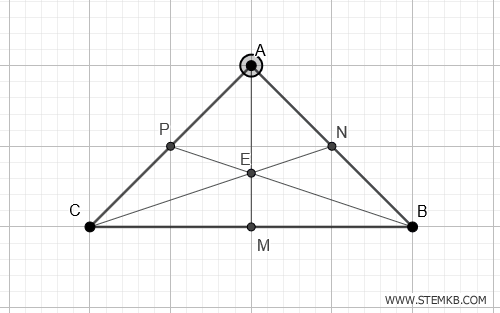
Quando tracci tutte e tre le mediane di un triangolo, scopri che queste si intersecano in un unico punto, detto baricentro.
Chiama questo punto E.
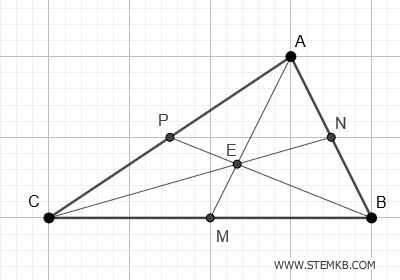
Il baricentro non è un semplice incrocio di linee, è il centro di gravità del triangolo, il punto in cui, se poggiassi il triangolo su una punta si bilancerebbe perfettamente in equilibrio.
Qualunque sia la forma o la dimensione del triangolo, le mediane si incontrano sempre nel baricentro.
Inoltre, il baricentro è sempre un punto interno del triangolo.
In breve, la mediana è più di una semplice linea: è un percorso che conduce al centro di equilibrio di un triangolo, unendo angoli e lati in un'interazione armoniosa.