Il punto in geometria

Quando pensi alla geometria, sicuramente ti vengono in mente delle figure complesse come triangoli, cerchi o poligoni. Tuttavia, ogni figura geometrica è a sua volta composta da elementi più semplici. Ogni figura prende forma da un'entità semplice e fondamentale della geometria: il punto.

In termini geometrici, il punto è un oggetto senza dimensioni.

Nella sua essenza, il punto è un concetto puro, privo di forma o misura. Non ha lunghezza, larghezza o altezza, né volume o superficie o altre grandezze di ogni tipo.

L'unica caratteristica del punto è la sua posizione.

Spesso nelle rappresentazioni grafiche lo visualizziamo come un piccolo cerchio per identificarlo meglio. In realtà, un punto non ha forma, né dimensione.

Per identificare un punto nel piano cartesiano siamo abituati a indicare le sue coordinate nel piano (x;y) o nello spazio (x;y;z).

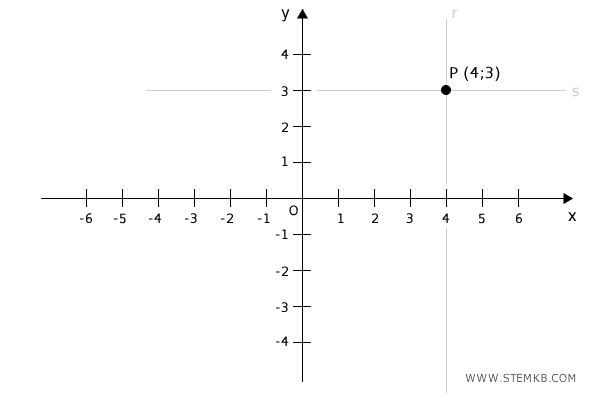
Pertanto, in termini matematici il punto può essere definito semplicemente da una coppia di coordinate in uno spazio bidimensionale o da una terna di coordinate in uno spazio tridimensionale.

Due punti A e B coincidono se occupano la stessa posizione $ A \cong B $.

Il punto è uno degli elementi fondamentali della geometria

Se ci pensi ogni figura è composta da un insieme infinito di punti. Senza punti, non ci sarebbero linee o piani.

Ad esempio, due punti definiscono una linea retta.

Quando tre punti appartengono alla stessa retta sono detti punti allineati.

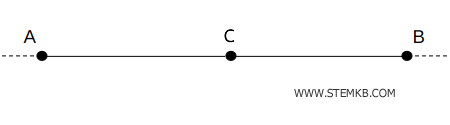
Tre punti distinti definiscono un piano se non sono allineati.

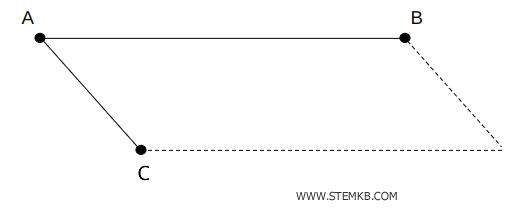
Con l'aggiunta di ulteriori punti, possiamo delineare forme e strutture sempre più complesse.

L'insieme di tutti i punti esistenti è chiamato spazio. L'idea di spazio può comunque variare in base al contesto scientifico

Pertanto, il punto è come un "mattone" nel mondo della geometria. Anche se, individualmente, ti può sembrare insignificante, è la combinazione di questi "mattoni" che crea il tessuto di ogni struttura geometrica.

Il punto un ente geometrico fondamentale (ente primitivo della geometria) perché è implicitamente definito dai postulati di Euclide.

Questi postulati, o assiomi, sono le affermazioni di base su cui si costruisce l'intera struttura della geometria. Questo approccio era comune nella matematica antica. Gli enti fondamentali venivano accettati come concetti intuitivi e non venivano definiti in termini di altre entità, né richiedono una dimostrazione. Invece, le loro proprietà venivano stabilite attraverso assiomi. Questi postulati formano le fondamenta su cui è costruita l'intera struttura della geometria euclidea. Oltre al punto, anche la retta e il piano sono enti fondamentali della geometria.

Sebbene la definizione pura di un punto possa sembrare astratta, i punti hanno molte applicazioni pratiche.

Ad esempio, in cartografia, i punti sono utilizzati per rappresentare posizioni specifiche sulla Terra.

Gli assiomi e le proprietà del punto nella geometria euclidea

Nel contesto della geometria euclidea, il punto interagisce strettamente con altre figure geometriche essenziali, come le rette e i piani.

Ecco alcune proprietà fondamentali che riguardano i punti sul piano euclideo.

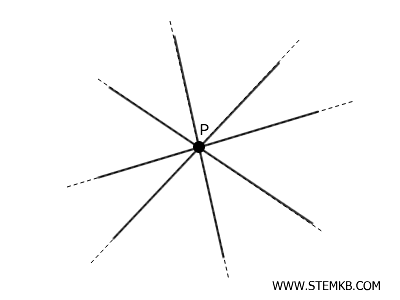
• Per un punto situato sul piano passano un numero illimitato di rette
  Un punto sul piano appartiene a infinite rette. Queste rette possono avere qualsiasi inclinazione o direzione. Questo assioma descrive una proprietà fondamentale dei punti e delle rette nella geometria euclidea.
  
• Tra due punti distinti passa, una e una sola retta
  Due punti distinti determinano un'unica retta che li collega. Questo assioma è fondamentale nella geometria euclidea.
  
• Per tre punti non allineati giace uno e un solo piano
  Tre punti non allineati definiscono un piano univoco nello spazio. Questo piano contiene tutti e tre i punti. È un assioma che descrive come i piani sono definiti nella geometria euclidea.
  

  

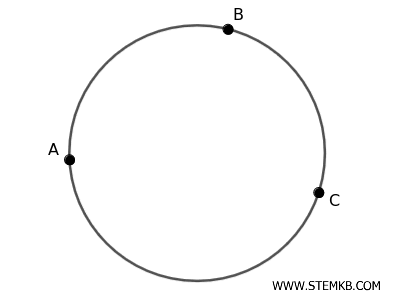
• Per tre punti non allineati passa una e una sola circonferenza
  È sempre possibile disegnare una circonferenza che passi esattamente per tre punti non allineati. Questa proprietà è una conseguenza logica degli assiomi e non un assioma in sé. È dimostrabile attraverso la geometria euclidea. Quindi, è un teorema.
  
• Una retta o una linea può essere considerata come una serie continua e infinita di punti
  Una retta è composta da un insieme infinito di punti disposti linearmente senza interruzioni. Questo assioma descrive la natura delle rette nella geometria euclidea.