Problema di geometria triangoli 1

Dato un triangolo ABC, l'angolo in A misura 60° e l'angolo in C misura 78°. Se BD è la bisettrice dell'angolo al vertice B, quale è la misura di ciascun angolo x e y che si forma al vertice B a causa della bisettrice?

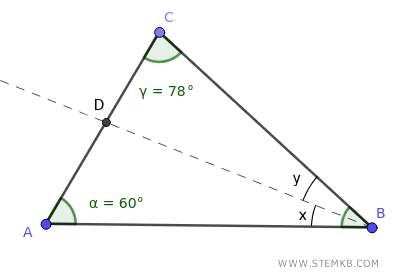
Soluzione svolta

Dato un triangolo ABC con angoli ai vertici A e C rispettivamente pari a 60° e 78°, puoi trovare l'angolo al vertice B utilizzando la somma degli angoli interni di un triangolo, che è sempre uguale a 180°:

$$ C \hat{A} B + A \hat{B} C + B \hat{C} A =180° $$

Sostituisci i valori dati dell'angolo A=60° e dell'angolo C=78°

$$ 60°+A \hat{B} C +78°=180° $$

$$ A \hat{B} C +138°=180° $$

Sottrai 138° da entrambi i membri dell'equazione

$$ A \hat{B} C +138°-138°=180°-138° $$

$$ A \hat{B} C =180°−138° $$

$$ A \hat{B} C =42° $$

Poiché il segmento BD è la bisettrice dell'angolo B, divide l'angolo B in due angoli congruenti.

Pertanto, ciascuno dei due angoli formati dalla bisettrice sarà:

$$ \frac{ A \hat{B} C }{2} = \frac{42°}{2} =21° $$

Quindi, gli angoli x e y della bisettrice nel vertice B sono entrambi 21°

$$ x = 21° $$

$$ y = 21° $$

Questa è la soluzione del problema.