Le figure congruenti

Nel mondo della geometria, termini come "uguale" e "congruente" sembrano a prima vista intercambiabili, ma in realtà nascondono differenze profonde. Approfondiamo insieme il concetto di figure congruenti e la loro differenza rispetto alle figure uguali.

Le figure uguali

Le figure uguali sono quelle composte dagli stessi punti, collocati nello stesso ordine e nella stessa posizione.

In altre parole, si tratta di copie perfette l'una dell'altra, senza alcuna trasformazione.

Ad esempio, se disegniamo due triangoli identici nello stesso punto del piano cartesiano, con vertici coincidenti, questi saranno sia uguali che congruenti.

Le figure congruenti

Le figure congruenti, invece, si distinguono perché possono essere sovrapposte punto a punto tramite movimenti rigidi, anche se si trovano in posizioni diverse o orientate in modi differenti.

Per indicare la congruenza si utilizza il simbolo $ \cong $.

Ad esempio, se abbiamo due figure A e B nel piano che possiamo spostare e sovrapporre esattamente l'una sull'altra, senza lasciare spazi vuoti, queste sono figure congruenti. In questo caso possiamo scrivere $ A \cong B $

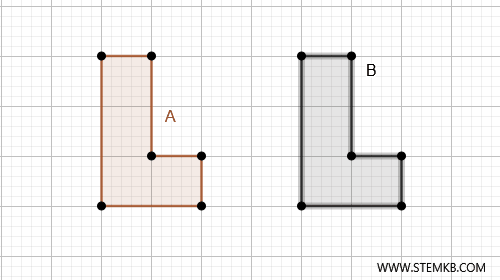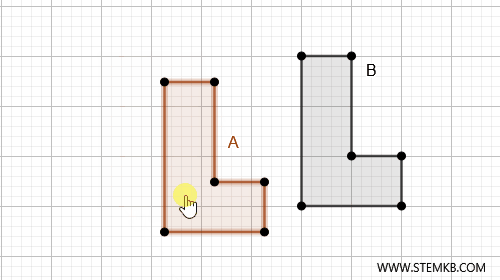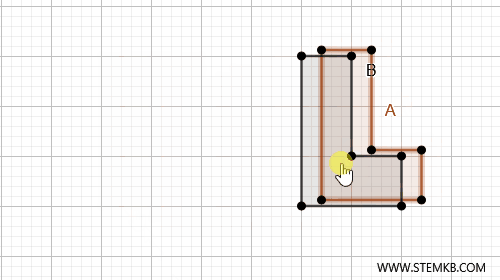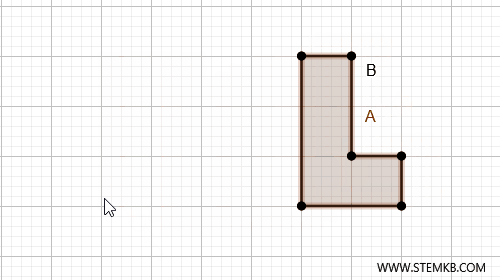
La congruenza si basa su due caratteristiche fondamentali:

• Stessa forma
• Stessa dimensione

Questo significa che due figure congruenti possono sembrare diverse a prima vista, ma esiste un movimento che le porta a coincidere perfettamente.

Quali sono i movimenti rigidi?

I movimenti rigidi sono le trasformazioni geometriche che preservano forma e dimensione, rendendo due figure congruenti. Ecco i principali:

• Traslazione
  Un movimento in linea retta che sposta una figura senza ruotarla né rifletterla. Ad esempio, se spostiamo una figura di qualche centimetro, facendola strisciare sul piano, la figura resta identica nella forma e nella dimensione.
  
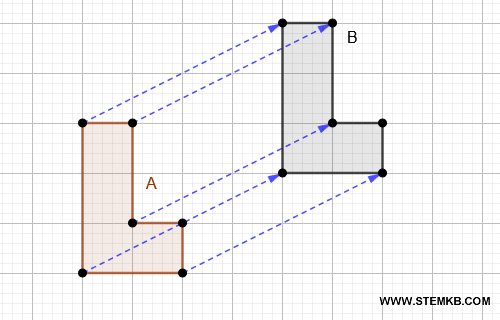
• Rotazione
  Una rotazione intorno a un punto fisso, mantenendo invariata la forma. Ad esempio, facciamo girare una figura di 180° intorno a un punto che scegliamo come centro di rotazione. Dopo la rotazione, la figura è congruente alla sua posizione originale perché ha la stessa forma e dimensione.
  
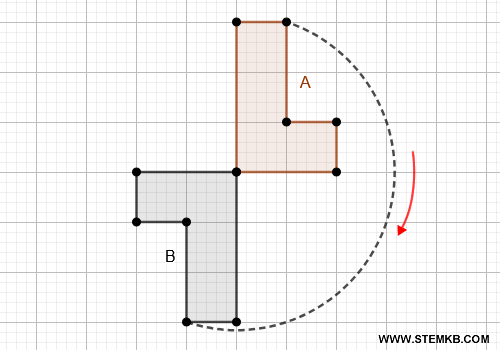
• Riflessione
  Una figura viene specchiata rispetto a una linea. Ad esempio, riflettere una figura rispetto a un asse di simmetria produce una figura congruente. La figura riflessa ha la stessa forma e dimensione della figura originale anche se è disposta in modo diverso.
  

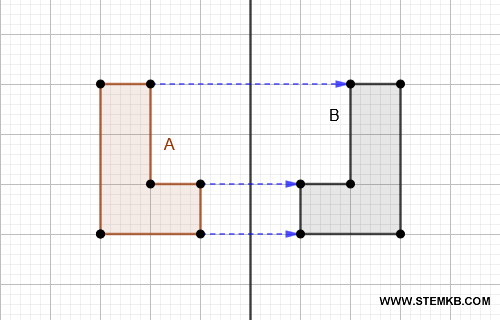
La differenza chiave tra figura uguale e congruente. Le figure uguali sono già sovrapposte perché sono composte esattamente dagli stessi punti. Le figure congruenti, invece, possono essere sovrapposte solo grazie ai movimenti rigidi. In sintesi, "uguale" implica la coincidenza esatta nei punti e nella posizione, "congruente" implica coincidenza nella forma e nella dimensione, ma non necessariamente nei punti o nella posizione. Quindi, due figure uguali sono anche congruenti ma due figure congruenti non è detto che siano anche uguali.

Le figure congruenti ci insegnano a guardare oltre l'apparenza superficiale, esplorando le relazioni geometriche e le trasformazioni che uniscono oggetti diversi.

Quando osserviamo figure apparentemente diverse, potremmo scoprire che, attraverso un semplice movimento, sono più simili di quanto immaginiamo.

Gli assiomi della congruenza

Gli assiomi della congruenza sono principi fondamentali della geometria euclidea che regolano le proprietà e i criteri per determinare quando due figure o segmenti geometrici possono essere considerati congruenti.

Vediamo insieme quali sono gli assiomi principali della congruenza e come vengono applicati.

• Primo assioma della congruenza: la riflessività
  Ogni figura geometrica è congruente a sé stessa. $$ A \cong A $$ Un segmento o un angolo è sempre congruente a sé stesso. Questo assioma può sembrare ovvio, ma è essenziale per stabilire una base logica.

  Ad esempio, un segmento \( AB \) sarà congruente a sé stesso (\( AB \cong AB \)). Allo stesso modo, un angolo di \( 60^\circ \) è congruente a \( 60^\circ \).
  

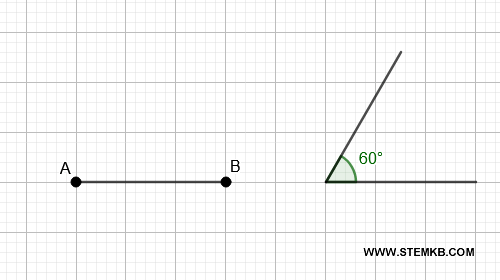
• Secondo assioma della congruenza: la simmetria
  Se una figura \( A \) è congruente a una figura \( B \), allora anche la figura \( B \) è congruente a \( A \). $$
  \text{Se } A \cong B \text{, allora } B \cong A $$

  Ad esempio, se un triangolo equilatero \( \triangle ABC \) è congruente a un altro triangolo equilatero \( \triangle DEF \), allora vale anche il viceversa.
  

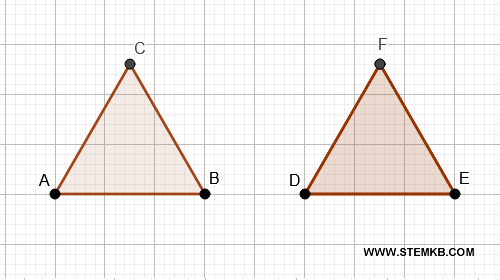
• Terzo assioma della congruenza: la transitività
  Se una figura \( A \) è congruente a una figura \( B \), e la figura \( B \) è congruente a una figura \( C \), allora anche \( A \) è congruente a \( C \). $$ \text{Se } A \cong B \text{ e } B \cong C \text{, allora } A \cong C $$

  Ad esempio, se un segmento \( AB \) è congruente al segmento \( CD \), e \( CD \) è congruente al segmento \( EF \), allora \( AB \) è congruente a \( EF \).
  

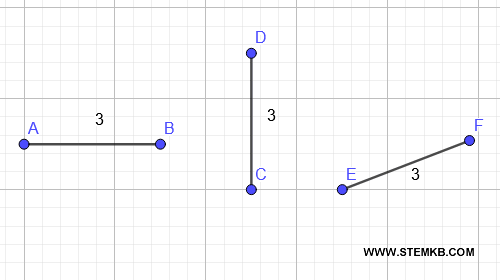
• Congruenza di punti
  Tutti i punti sono congruenti fra loro. Quindi, deduciamo che sono congruenti tra loro anche le rette, le semirette, i piani e i semipiani perché sono composti da punti.

Gli assiomi della congruenza sono i mattoni su cui si costruisce la geometria euclidea. Riflessività, simmetria e transitività ci offrono un linguaggio chiaro per descrivere e confrontare figure geometriche.

Oltre a questi assiomi generali ci sono anche diverse regole di congruenza che si applicano solo per figure specifiche. Ad esempio, i criteri di congruenza dei triangoli ci permettono di capire se due triangoli sono congruenti o meno.

Questi principi sono universali nella geometria e trovano applicazione in molteplici ambiti.