Geometria

La geometria è una branca della matematica che si occupa dello studio delle forme, delle dimensioni e delle proprietà dello spazio.

La parola "geometria" ha origini greche e significa letteralmente "misura della terra".

Questa scienza ha radici antiche e diverse civiltà, come egizi, cinesi, babilonesi, romani e greci, l'hanno utilizzata per vari scopi pratici come la misurazione del terreno, la navigazione e l'osservazione delle stelle.

Gli antichi egizi usavano la geometria nella costruzione delle piramidi, nella ridefinizione dei confini agricoli dopo le inondazioni del Nilo e nell'astronomia. I babilonesi raccolsero diversi problemi geometrici sulle loro tavolette cuneiformi e la utilizzavano prevalentemente nell'astronomia. I cinesi la usarono nella divisione delle terre agricole e nell'architettura. I greci integrarono la geometria nella filosofia e nell'architettura. I romani, infine, la usarono soprattutto nell'ingegneria (acquedotti, strade), nell'urbanistica e nell'arte.

I greci, in particolare, hanno avuto un ruolo fondamentale nello sviluppo della geometria come la conosciamo oggi. Hanno cercato di organizzare e razionalizzare le conoscenze geometriche attraverso ragionamenti logici e dimostrazioni.

Alcuni filosofi e matematici greci, come Thales, Pitagora, Platone e Aristotele, hanno contribuito significativamente a questo campo.

Tuttavia, è Euclide che ha scritto "Elementi", un testo che raccoglie e organizza le conoscenze geometriche dell'epoca. Questo libro è così fondamentale che è stato utilizzato come testo di riferimento per la geometria per oltre 2000 anni.

Per questo motivo, la "geometria piana" è oggi conosciuta come "geometria euclidea" in onore di Euclide.

Gli enti fondamentali della geometria

Oggi quando parliamo di geometria, ci riferiamo soprattutto a quella "piana" (sulle superfici piatte) e quella "spaziale" (nello spazio tridimensionale). Dove per spazio si intende tutto ciò che ci circonda. Ha tre dimensioni: lunghezza, larghezza e altezza.

I concetti primitivi della geometria sono il punto, la retta e il piano.

• Punto
  È come un piccolo segno. Non ha dimensioni, né lunghezza, né larghezza, né altezza. È solo un oggetto che occupa una posizione nello spazio.
  
• Retta
  Immagina una linea dritta che si estende all'infinito in entrambe le direzioni. Questa è una retta. Ha una sola dimensione: la lunghezza.
  
• Piano
  È come un foglio di carta infinitamente grande. Ha due dimensioni: lunghezza e larghezza.
  

Quando combiniamo questi elementi, otteniamo altre forme come segmenti (parti di una retta), angoli (dove due rette si incontrano), le figure geometriche, poligoni (come triangoli e quadrati) e poliedri (come cubi e piramidi).

Inoltre, non tutte le forme sono piatte. Alcune figure geometriche sono curve. Ad esempio, il cerchio, le ellissi, ecc.

Ma la geometria non si ferma qui. Usando matematica avanzata, puoi esplorare spazi con più di tre dimensioni, anche se non possiamo vederli o immaginarli facilmente. Questi sono chiamati spazi vettoriali.

Infine, non tutte le geometrie seguono le stesse regole. La maggior parte delle regole che conosciamo proviene dalla geometria di Euclide (geometria euclidea).

Ricorda però che ci sono anche geometrie dove queste regole non si applicano, chiamate geometrie non euclidee.

Un esempio di geometria non euclidea è la superficie del nostro pianeta. Se prendi un triangolo sulla superficie terrestre, può avere proprietà diverse da un triangolo su un foglio di carta piatto.

L’evoluzione della geometria dal metodo induttivo al metodo deduttivo

Immagina di osservare il mondo attorno a te: le forme delle montagne, i profili degli edifici, il cerchio disegnato nell’acqua da un sasso.  Questa è la geometria delle origini, nata dall’intuizione e dall’esperienza diretta.

Nel passato, chi studiava la geometria seguiva un approccio induttivo: partiva dall’osservazione di fenomeni concreti e ripetibili per identificare generalizzazioni note come congetture.

Ad esempio, dopo aver misurato gli angoli di numerosi triangoli, si poteva congetturare che la somma degli angoli interni di un triangolo è sempre 180°.

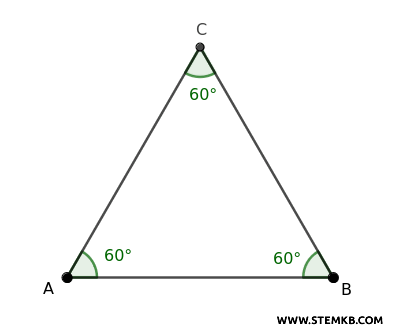
Le congetture erano proposizioni che risultavano credibili grazie alla ripetitività dei fenomeni osservati, ma non erano ancora dimostrate formalmente.

Tuttavia, l’approccio induttivo presentava un limite: non poteva garantire che una proprietà fosse valida in tutti i casi, ma solo in quelli osservati.

Con l’avanzare della conoscenza, la geometria richiese maggiore rigore. Non bastava sapere che un’idea "sembrava" vera: bisognava dimostrarlo.

Ad esempio, se disegni un triangolo su una superficie curva, come una sfera, la somma degli angoli può essere maggiore di 180°. Se invece lo disegni su una superficie concava, la somma degli angoli è inferiore a 180°. Quindi, in generale, non è detto che la somma degli angoli di un triangolo sia sempre uguale a un angolo piatto, perché dipende dalla superficie su cui viene disegnato (piana, concava o convessa).

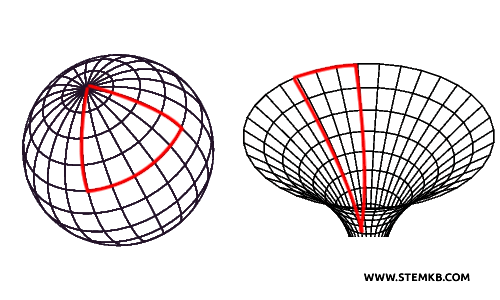
Quindi entrò in scena il metodo deduttivo, che trasforma la geometria in una scienza logica, fondata su assiomi e dimostrazioni.

L’approccio deduttivo parte da alcuni presupposti fondamentali:

• Concetti primitivi: sono termini non definiti ma accettati come intuitivi, come il "punto" o la "retta". Questo è necessario perché per scrivere una definizione di questi primi enti geometrici, come il punto o la retta, dovremmo usare altri termini che a loro volta dovrebbero essere definiti, entrando in un circolo vizioso.
• Assiomi o postulati: sono proposizioni assunte vere senza dimostrazione, come "per due punti distinti passa una e una sola retta". In altre parole, sono accettati come vere senza dare alcuna giustificazione.
• Definizioni: sono nuovi termini che spiegano oggetti matematici più complessi, come il "triangolo" o il "parallelogramma". La loro definizione si basa sui concetti primitivi, sugli assiomi e su altre definizioni precedentemente stabilite.
• Teoremi: sono affermazioni dimostrate a partire dagli assiomi mediante il ragionamento logico detto "dimostrazione". Quindi, sono enunciati veri che si deducono per dimostrazione da altre proposizioni.

Un esempio classico è il sistema di Euclide, un matematico greco che nel III secolo a.C. strutturò la geometria secondo il metodo assiomatico-deduttivo.

Nei 13 libri chiamati "Elementi" Euclide stabilì i cinque assiomi fondamentali e costruì l’intera geometria euclidea dimostrando teoremi passo dopo passo.

Ad esempio, Euclide assume che una retta può essere tracciata tra due punti e che una retta taglia due parallele formando angoli uguali.

Questo nuovo metodo non solo rese la geometria più rigorosa, ma ne ampliò gli orizzonti. Dimostrò che non era necessario osservare ogni caso specifico per affermare una proprietà generale: bastava dedurla logicamente.

Inoltre, aprì la strada alla nascita delle geometrie alternative o "non euclidee", come la geometria sferica e la geometria iperbolica, dove gli assiomi euclidei vennero modificati.

In conclusione, l’approccio induttivo rimane il punto di partenza naturale per chi si avvicina alla geometria: osservare, intuire, congetturare.

Tuttavia, è il metodo assiomatico-deduttivo a conferire alla geometria il suo carattere scientifico, garantendo che ogni verità sia rigorosamente dimostrata.

Questo passaggio dalla congettura alla dimostrazione trasforma la geometria in una scienza universale e logica, capace di spiegare il mondo e persino di superarne i limiti osservabili.