La risultante tra le forze
Cos’è la risultante delle forze?
La forza risultante è la somma vettoriale delle singole forze che agiscono su un oggetto. $$ \vec{R} = \vec{F}_1 + \vec{F}_2 $$
A differenza della somma scalare, nel caso dei vettori, bisogna tenere conto sia della direzione che del verso delle forze coinvolte.
La risultante determina l’effetto complessivo prodotto da più forze che agiscono simultaneamente.
E' un concetto fondamentale nella fisica e ci aiuta a comprendere l’equilibrio degli oggetti e il loro movimento.
Un esempio
Immaginiamo di osservare un libro fermo su un tavolo: sembra immobile, ma in realtà su di esso agiscono almeno due forze.
Una forza $ \vec{F_1} $ è quella della gravità, che spinge il libro verso il basso; l’altra forza $ \vec{F_2} $ è la reazione vincolare del tavolo, una forza che agisce verso l’alto, opponendosi alla gravità.
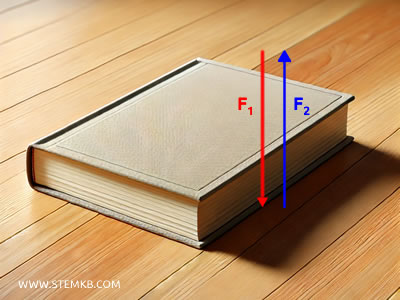
Le due frecce sono i vettori che rappresentano le due forze, la loro direzione e il loro verso. La lunghezza delle frecce misura l'intensità di ciascuna forza.
La somma dei vettori può essere rappresentata graficamente tracciando i vettori (le frecce) uno dopo l’altro, come se li “mettessimo in fila”. La risultante è il vettore che collega l’inizio del primo vettore con la fine dell’ultimo.
Perché il libro non si muove?
Perché queste due forze si bilanciano perfettamente, e la loro somma vettoriale è zero.
Questa è la chiave per comprendere il concetto di risultante delle forze. La somma vettoriale tra queste due forze è nulla $ \vec{F_1} + \vec{F_2} = \vec{0} $.
In questo caso i due vettori hanno la stessa intensità (lunghezza) e sono opposti, quindi la fine dell'ultimo vettore (freccia blu) coincide con l'inizio del primo vettore (freccia rossa).
Quando la risultante delle forze è nulla, si dice che il sistema è in equilibrio. E' un caso particolare di risultante che analizzeremo più approfonditamente nel prossimo paragrafo.
Esempio 2
Quando un arciere tende la corda dell'arco e la rilascia, possiamo immaginare che sulla freccia agiscano due forze uguali in modulo ma dirette obliquamente rispetto alla freccia.
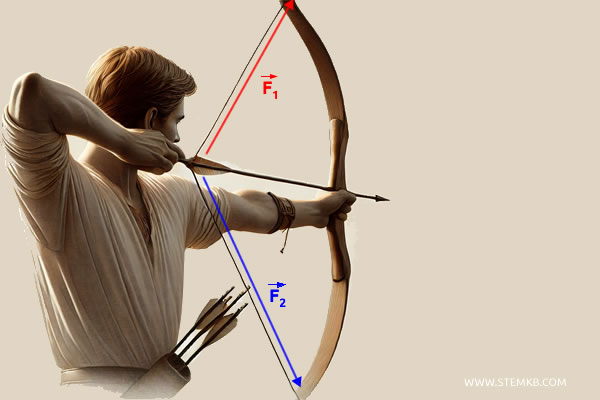
Tracciamo i due vettori \( \vec{F}_1 \) e \( \vec{F}_2 \) a partire dallo stesso punto.
- La forza della corda sul lato destro (vettore \( \vec{F}_1 \)), che agisce inclinata verso sinistra.
- La forza della corda sul lato sinistro (vettore \( \vec{F}_2 \)), inclinata verso destra.
Queste due forze, essendo simmetriche e opposte tra loro rispetto alla freccia, formano un angolo alla loro intersezione.
Per determinare la risultante delle due forze, possiamo calcolare la somma dei due vettori usando il metodo del parallelogramma.
Completiamo il parallelogramma disegnando le linee parallele ai due vettori.
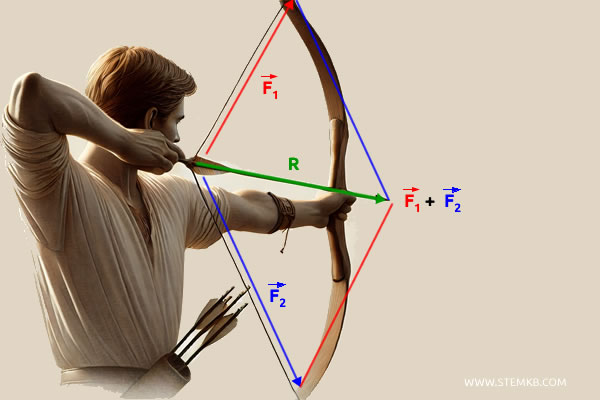
La diagonale del parallelogramma, che parte dall'origine comune dei due vettori, rappresenta la risultante delle forze \( \vec{R} \).
$$ \vec{R} = \vec{F_1} + \vec{F_2} $$
In questo esempio, la risultante \( \vec{R} \) coincide con la direzione della freccia e punta in avanti, lungo l'asse centrale dell'arco.
In altre parole, le due forze oblique \( \vec{F}_1 \) e \( \vec{F}_2 \) si "combinano" vettorialmente per produrre una forza risultante che spinge la freccia in avanti. Questo avviene perché le componenti orizzontali delle due forze si sommano, mentre le componenti verticali (opposte) si annullano a vicenda. Il risultato finale è un vettore risultante orizzontale, che coincide con il moto della freccia.
Questo esempio illustra perfettamente come, in pratica, la somma vettoriale di più forze determini il moto di un oggetto.
Equilibrio delle forze
Un caso molto interessante si verifica quando la somma vettoriale delle forze è il vettore zero.
$$ \vec{R} = \vec{F_1} + \vec{F_2} = \vec{0} $$
In questo caso, la risultante delle forze è nulla e l’oggetto è in equilibrio.
Questa situazione può succedere anche se le forze individualmente non sono nulle.
Ad esempio, due persone tirano una fune in direzioni opposte con la stessa forza $ | \vec{F_1} | = | \vec{F_2} | $.
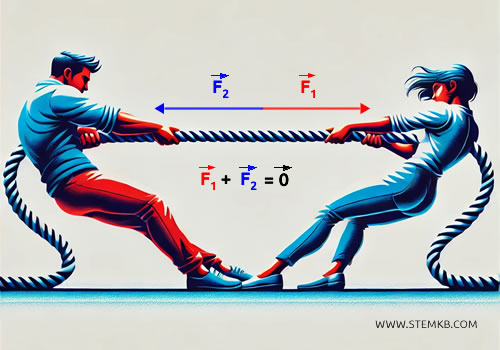
La corda non si muove malgrado le persone continuino a tirare da una parte e dall'altra, esercitando due forze uguali ma contrapposte.
Questo accade perché la risultante delle forze è il vettore nullo $ \vec{F_1} + \vec{F_2} = \vec{0} $ e le forze sono in equilibrio
La situazione cambierebbe se uno dei due gruppi applicasse una forza diversa dall'altro gruppo. In questo caso, la corda inizierebbe a spostarsi verso il gruppo che applica la forza maggiore. Quindi, la capacità di calcolare la risultante delle forze ci permette non solo di descrivere lo stato di un corpo ma anche di prevederne il comportamento futuro, aprendo la strada a infinite applicazioni pratiche.
Il bilanciamento delle forze è alla base di molte altre situazioni quotidiane e fenomeni naturali.
Spesso non ce ne accorgiamo perché li riteniamo "normali" ma esistono diversi fenomeni naturali in cui possiamo l'equilibrio di due forze. Ad esempio, il lampadario al soffito, un vaso al centro di un tavolo, un ponte che attraversa un fiume, ecc.
FAQ
- Può la risultante di due forze di intensità diverse essere nulla?
No, se le forze hanno intensità diversa, la loro somma vettoriale non può essere zero. Per avere una risultante nulla, le forze devono avere stessa intensità, stessa direzione, ma verso opposto. - Può la risultante di tre forze di intensità diverse essere nulla?
Sì, è possibile. Affinché la risultante di tre forze sia nulla, esse devono essere disposte in modo tale da bilanciarsi tra loro, formando un triangolo chiuso quando rappresentate graficamente. Questo avviene quando le tre forze soddisfano la condizione di equilibrio vettoriale.Ad esempio, questi vettori $ \vec{u} $, $ \vec{v} $, e $ \vec{w} $ rappresentano tre forze.
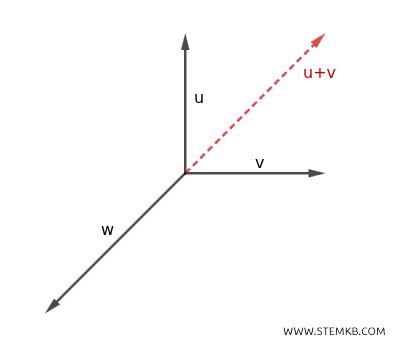
La somma delle tre forze è nulla $$ \vec{u} + \vec{v} + \vec{w} = \vec{0} $$ Per dimostrarlo geometricamente basta osservare che la somma dei vettori $ \vec{u} + \vec{v} $ è uguale al vettore opposto di $ \vec{w} $ $$ \vec{u} + \vec{v} = - \vec{w} $$ La somma di un vettore con il suo vettore opposto è sempre uguale al vettore nullo. Pertanto, la risultante delle tre forze è nulla. $$ ( \vec{u} + \vec{v} ) + \vec{w} = - \vec{w} + \vec{w} = \vec{0} $$