Il centro di massa
Il centro di massa è un punto ideale in cui puoi immaginare concentrata tutta la massa di un corpo o di un sistema di corpi.
Quando studi il movimento di un oggetto esteso, puoi immaginare che tutto il corpo si comporti come se fosse concentrato in un solo punto: il centro di massa.
Il centro di massa è un punto geometrico astratto, non necessariamente occupato da materia. Quindi, può essere associato a una massa oppure no.
In genere, coincide con il baricentro quando il corpo ha massa distribuita in modo omogeneo.
Nei modelli semplificati è il punto dove si applica la forza peso e si sposta come se tutte le forze esterne agissero su di lui.
Quando si usa? Serve a semplificare l’analisi del moto, delle forze e dell’equilibrio di oggetti anche molto complessi. Il concetto di centro di massa è utile quando devi calcolare le forze totali che agiscono su un corpo, studiare il moto traslatorio indipendentemente dalla rotazione, analizzare l’equilibrio statico e dinamico, determinare se un oggetto cadrà o resterà in piedi, ecc.
Esempi Pratici
Esempio 1 (corpo omogeneo)
Un cubo di legno pieno e perfettamente omogeneo ha il suo centro di massa esattamente al centro del cubo.
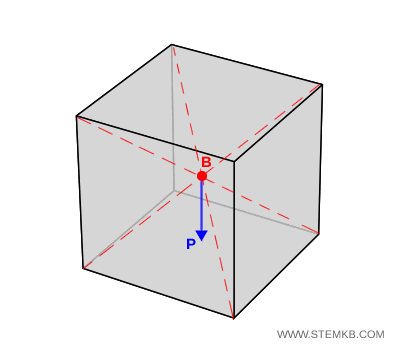
Questo accade perché la sua massa è distribuita in modo omogeneo. Quindi, si considera il suo baricentro come centro di massa.
Se lo appoggi su una superficie piana, la forza peso $ \vec{P} $ agisce lungo la verticale passante per quel punto.
Esempio 2 (corpo cavo o non omogeneo)
Nel caso di un anello metallico o di una ciambella (solido toroidale), la massa è distribuita lungo il bordo.
In questo caso il centro di massa non coincide con la materia del corpo, ma si trova al centro del cerchio, ossia nel vuoto.

Esempio 3 (due masse collegate)
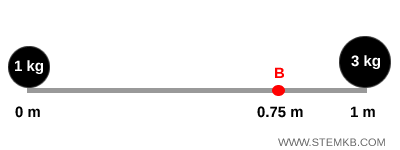
Due palline, una da 1 kg e una da 3 kg, collegate da una barra leggera lunga 1 m.

In questo caso, il centro di massa si calcola con la formula:
$$ x_{cm} = \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2} $$
Poiché $x_1 = 0$ e $x_2 = 1$, allora:
$$ x_{cm} = \frac{1\cdot0 + 3\cdot1}{1+3} = \frac{3}{4} = 0{,}75\ \text{m} $$
il centro di massa si trova a 75 cm dalla pallina leggera. Quindi, è molto più vicino alla pallina più pesante.
In generale, per un sistema di particelle puntiformi si utilizza questa formula $$ \vec{R}_{cm} = \frac{\sum m_i \vec{r}_i}{\sum m_i} $$ Dove $m_i$ sono le masse dei singoli punti, $\vec{r}_i$ sono le loro posizioni nello spazio.
In conclusione, il centro di massa è uno strumento essenziale in fisica per ridurre problemi complessi a modelli più semplici.
Che si tratti di una palla che cade o di un satellite in orbita, basta sapere dove si trova il centro di massa per capire come si muoverà tutto il sistema.