Equilibrio di un punto materiale
Un punto materiale è un modello ideale di corpo con massa, ma senza dimensioni. Per capire quando è in equilibrio, occorre osservare se resta perfettamente fermo nel tempo, cioè non si muove né trasla.
La condizione fondamentale è che la somma delle forze è nulla
La condizione necessaria (e anche sufficiente) affinché un punto materiale sia in equilibrio statico è molto semplice da esprimere:
$$ \vec{R} = \sum \vec{F}_i = 0 $$
Significa che tutte le forze che agiscono sul punto devono annullarsi tra loro, cioè la risultante vettoriale deve essere zero.
Non importa quante forze siano in gioco: ciò che conta è che la loro somma vettoriale sia zero.
$$ \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \dots + \vec{F}_n = 0 $$
Esempio
Ad esempio, una tazza di latte appoggiata sul tavolo non si muove.
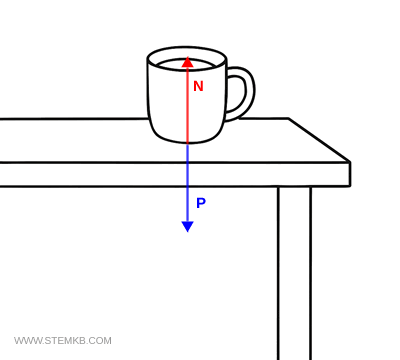
Le forze agenti su di essa sono:
- la forza peso $ \vec{P} $ che la spinge verso il basso (verso il centro della Terra), con modulo $ P = mg $.;
- la reazione normale $ \vec{N} $ del tavolo, che spinge con uguale intensità verso l’alto.
Le due forze si bilanciano perfettamente:
$$ \vec{P} + \vec{N} = 0 $$
Quindi, la tazza è in equilibrio statico.
Quali forze vanno considerate? Quando si parla di equilibrio, non serve considerare tutte le forze possibili, ma solo quelle effettivamente applicate al corpo. Le principali sono la forza peso ( $\vec{P} $) che è sempre diretta verso il basso, e lereazioni vincolari ($ \vec{R}_v $) che dipendono dal tipo di vincolo (tavolo, parete, filo...) e servono a impedire il movimento.
Ti faccio un altro esempio.
Guarda un lampadario sospeso al soffitto.
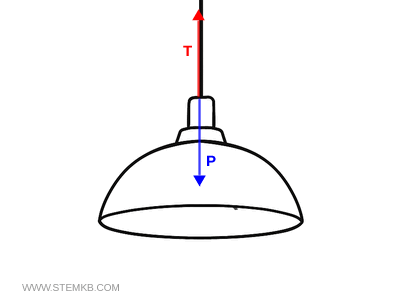
Sul lampadario agiscono due forze:
- La forza peso $ \vec{P} $ che agisce verso il basso,
- La tensione $ \vec{T} $ del filo verso l’alto.
Se le due forze sono uguali in modulo e opposte in direzione, il punto resta in equilibrio... e il lampadario non cade.
Cosa sono i vincoli? I vincoli sono ciò che impedisce al punto materiale di cadere, muoversi o ruotare. Ogni vincolo genera una reazione vincolare, che è una forza, nasce come risposta alla forza applicata e impedisce lo spostamento nella direzione bloccata.
E se il piano è inclinato?
Quando un oggetto è appoggiato su un piano inclinato, devi scomporre la reazione del piano in due parti:
- una componente normale $ \vec{N} $ alla superficie che bilancia il peso $ \vec{P_y} $ perpendicolare al piano;
- una componente parallela $ \vec{P_x} $ alla superficie che può essere contrastata dall’attrito statico $ \vec{S} $.
In questo caso il corpo non scivola se l'attrito statico $ S $ riesce a compensare la forza opposta parallela al piano $ P_x $ e se la reazione vincolare $ N $ riesce a sorreggere il peso della cassa $ P_y $ perpendicolare al piano.
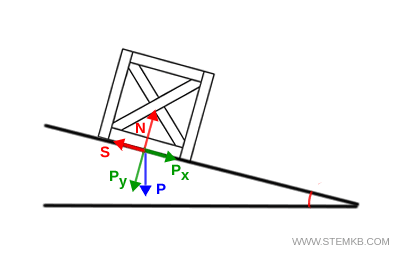
In altre parole, la cassa è in equilibrio se la somma delle forze è nulla sia sull'asse parallelo al piano $ P_x + S = 0 $ che su quello perpendicolare $ N + P_y = 0 $.