La forza elastica e la legge di Hooke
La legge di Hooke afferma che, entro certi limiti, la forza esercitata da una molla ideale è direttamente proporzionale al suo allungamento o compressione rispetto alla posizione di equilibrio. $$ \vec{F} = -k \vec{x} $$ dove \( \vec{F} \) è la forza applicata alla molla, \( k \) è una costante che indica la rigidità della molla, \( \vec{x} \) è lo spostamento della molla.
Immagina di tenere in mano una molla: la tiri e senti una resistenza che aumenta man mano che l’allunghi.
Questa forza "elastica" $ F $ agisce in senso contrario allo spostamento $ x $ e cerca di riportare la molla alla lunghezza iniziale $ L $.
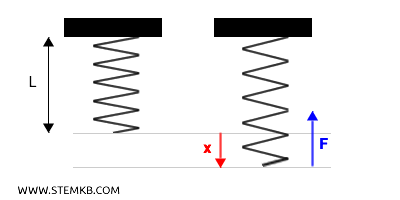
Questa forza non agisce solo quando allunghi la molla ma anche quando la comprimi.
Anche in questo caso la forza elastica $ F $ agisce in senso opposto allo spostamento $ x $ cercando di riportare la molla alla lunghezza iniziale $ L $.
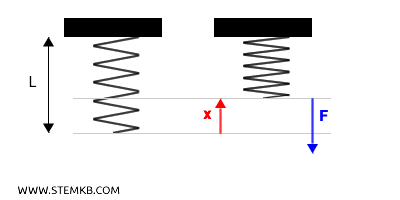
Nel XVII secolo, il fisico e naturalista inglese Robert Hooke formulò una legge semplice quanto rivoluzionaria per descrivere questo comportamento elastico dei materiali.
La legge di Hooke afferma che la forza esercitata da una molla ideale è direttamente proporzionale alla sua deformazione (allungamento o compressione) rispetto alla sua lunghezza naturale.
Matematicamente, la legge di Hooke di una "molla ideale" può essere espressa come:
$$ F = -kx $$
Dove:
- \( F \) è la forza elastica (diretta verso la posizione di equilibrio)
- \( x \) è la deformazione della molla rispetto alla sua lunghezza naturale (positiva per allungamento e negativa per compressione).
- \( k \) è la costante elastica della molla (detta anche costante di Hooke), che misura la rigidità della molla, misurata in newton per metro (N/m). Più alta è la costante \(k\), più "resistente" allo spostamento è la molla. Ad esempio, una molla d’acciaio rigido ha un valore di \(k\) molto maggiore rispetto a una molla morbida di plastica.
Il segno meno nella formula $ F = -kx $ indica che la forza elastica $ F $ si oppone sempre allo spostamento $ x $: una caratteristica fondamentale che permette alla molla di "ritornare in forma".
Cos'è una "molla ideale"? Una molla ideale è un modello teorico utilizzato in fisica per semplificare lo studio dei sistemi elastici. Si tratta di una molla priva di massa e attrito, che obbedisce perfettamente alla legge di Hooke in ogni condizione di utilizzo, purché non venga superato il limite elastico. Questo modello consente di concentrarsi esclusivamente sulla relazione tra forza applicata e spostamento, senza considerare la massa e le proprietà reali dei materiali usati per costruire la molla.
Poiché il verso della forza elastica cambia a seconda se la molla viene allungata o compressa, spesso la legge di Hooke viene scritta nella forma vettoriale.
$$ \vec{F} = -k \vec{x} $$
Dove \( \vec{F} \) è la forza elastica mentre \( \vec{x} \) è il vettore spostamento.
Oggi la legge di Hooke è una delle fondamenta della fisica classica e, dopo oltre tre secoli dalla sua scoperta, continua a offrire una descrizione precisa di come le molle e altri sistemi elastici rispondano alle forze applicate.
I limiti della legge di Hooke. Sebbene potente, la legge di Hooke ha però i suoi limiti. Funziona bene solo quando la deformazione è elastica, cioè quando la molla torna alla sua forma originale dopo essere stata allungata o compressa. Se lo spostamento è troppo grande, il materiale può deformarsi permanentemente, violando la proporzionalità e rendendo inapplicabile la legge. Ogni molla ha un limite elastico ben definito, oltre i quale il materiali possono deformarsi plasticamente (deformazione permanente) oppure rompersi.
Un esempio pratico
Hai una molla con una costante elastica \( k = 200 \, \text{N/m} \).
Vuoi calcolare la forza elastica che la molla esercita quando viene allungata di \( x = 0,1 \, \text{m} \) (10 cm).
La legge di Hooke si esprime in forma scalare come:
$$ F = k \cdot x $$
Inseriamo i valori:
$$ F = 200 \, \text{N/m} \cdot 0,1 \, \text{m} $$
$$ F = 20 \, \text{N} $$
Quindi, la forza elastica esercitata dalla molla è di 20 newton.
Questo significa che se applichi una forza di 20 N per allungare la molla di 10 cm, questa reagisce esercitando una forza elastica di 20 N, diretta verso la posizione di equilibrio.
In questo caso la costante \( k = 200 \, \text{N/m} \) indica che la molla è piuttosto rigida: per ogni metro di allungamento, occorrerebbero ben 200 newton di forza.
Esempio 2
Per capire meglio la legge, immaginiamo un esempio concreto: un dinamometro a molla, uno strumento di misura che traduce l’allungamento della molla in una misura della forza applicata.
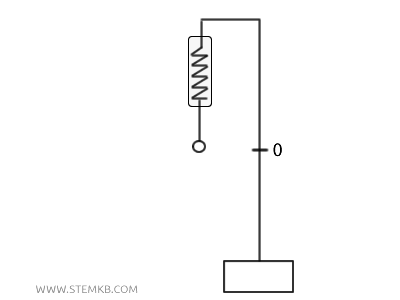
Quando appendi un peso all’estremo della molla, questa si allunga proporzionalmente al peso, e quindi alla forza gravitazionale esercitata sull’oggetto.
Supponiamo di avere una molla più morbida, con \( k = 50 \, \text{N/m} \), montata su un dinamometro.
Appendiamo un peso di \( m = 2 \, \text{kg} \).
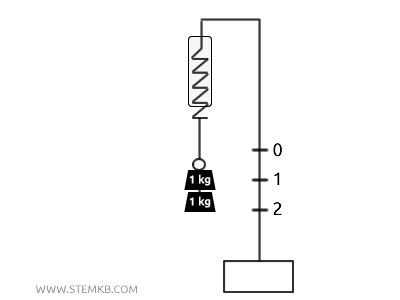
Quanto si allunga la molla?
Per prima cosa calcoliamo la forza $ F $ applicata dalla gravità sul peso.
$$ F = m \cdot g = 2 \, \text{kg} \cdot 9,8 \, \text{m/s}^2 = 19,6 \, \text{N} $$
A questo punto, usando la legge di Hooke (\( F = k \cdot x \)), possiamo calcolare l’allungamento \( x \):
$$ x = \frac{F}{k} = \frac{19,6 \, \text{N}}{50 \, \text{N/m}} = 0,392 \, \text{m} $$
In questo caso la molla si allunga di 39,2 cm.
Il dinamometro rappresenta solo una delle molteplici applicazioni pratiche della legge di Hooke, ma i principi che essa descrive trovano impiego in una vasta gamma di contesti che vanno ben oltre il semplice comportamento delle molle. Lo stesso principio si applica, ad esempio, nella progettazione di sospensioni per veicoli, nella costruzione di edifici antisismici, nei dispositivi medici come i pacemaker e persino nello studio delle vibrazioni molecolari in chimica e fisica.
In conclusione, questi esempi dimostrano come, a oltre 350 anni dalla sua scoperta, la legge di Hooke continui a essere uno strumento essenziale per risolvere molti problemi pratici e comprendere meglio il comportamento dei sistemi elastici.