Equilibrio di un corpo appeso a una corda

Immagina di sollevare un secchio d’acqua con una corda passata in una carrucola: sembra un gesto semplice, ma dietro questo movimento si nascondono concetti fondamentali della fisica, legati all’equilibrio e alla tensione. Vediamo insieme cosa succede.

La tensione in una corda

Quando una corda sottile viene tirata da due estremità con forze opposte e di uguale intensità, lungo tutta la sua lunghezza si stabilisce una tensione costante, che indichiamo con la lettera $ T $.

Se la massa della corda è trascurabile, la tensione è identica in ogni punto della corda.

Adesso, se idealmente tagliassimo la corda, la forza $ T $ sarebbe quella che continua a "tenere unite" le due estremità.

Un corpo appeso a una corda

Se appendiamo un corpo di peso $ P $, ad esempio, un lampadario, la corda lo sostiene esercitando una forza verso l’alto di intensità $ T = P $.

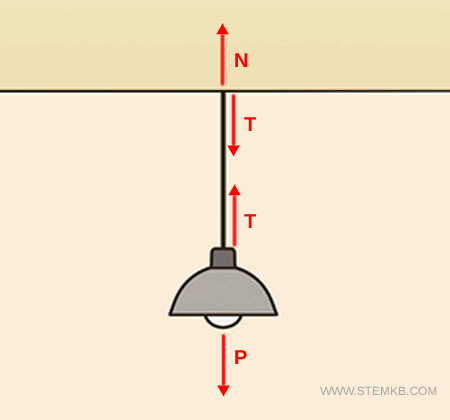
La tensione $ T $ si rileva anche all'altra estremità della corda, quella collegata al soffitto.

Allo stesso tempo, il punto di ancoraggio al soffitto esercita una reazione vincolare $ N $ uguale e contraria per mantenere l’equilibrio.

L'uso della carrucola

Una carrucola ideale (senza attriti né massa propria) non cambia l’intensità della tensione nella corda, ma ne devia la direzione.

Questo rende più comodo sollevare o regolare il carico.

Ad esempio, prendiamo il caso del secchio appeso tramite carrucola

Quando un secchio è appeso tramite una carrucola, sul secchio agiscono due forze:

• Il suo peso $ P $, diretto verso il basso.
• La tensione $ T_1 = P $, diretta verso l’alto attraverso la corda.

La persona che solleva il secchio deve applicare una forza verso il basso di intensità $ T_1 = P $ per mantenerlo fermo o sollevarlo lentamente.

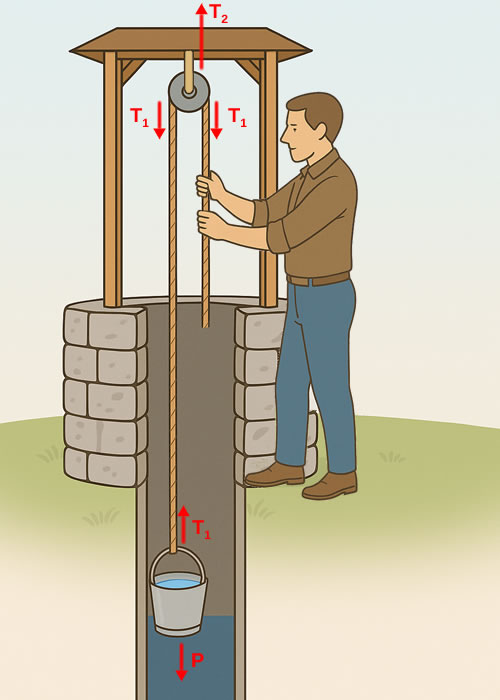
Anche la carrucola deve essere in equilibrio.

Pertanto, le forze che agiscono su di essa sono:

• Una forza $ T_2 $ verso l’alto, esercitata dal supporto che la sostiene.
• Due forze $ T_1 $ verso il basso: una dalla corda collegata al secchio e una dalla corda tirata dalla persona.

Perché la carrucola resti ferma, la condizione di equilibrio deve essere:

$$ T_2 = 2T_1 = 2P $$

Questo significa che la tensione che mantiene collegata la carrucola al soffitto è due volte il secchio.

Un principio chiave da ricordare. In una corda ideale, la tensione è costante lungo tutta la sua lunghezza, a meno che non ci siano elementi che la modificano (come attriti o masse distribuite lungo la corda).

Corde oblique: come si studia la tensione

Quando una o più corde sono inclinate, per determinare la tensione in ciascuna corda è necessario applicare le condizioni di equilibrio:

• Equilibrio verticale
  La somma delle componenti verticali delle tensioni deve bilanciare il peso del carico.
• Equilibrio orizzontale
  La somma delle componenti orizzontali delle tensioni deve essere zero (se il sistema è fermo).

Ad esempio, immagina un carico di peso \$ P = 100 \ N \$ appeso a due corde, che formano angoli \$ \theta_1 =30% \$ e \$ \theta_2 = 45° \$ con l’orizzontale.

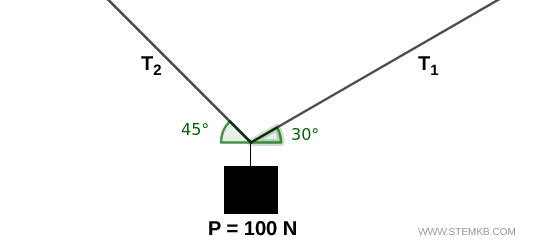
Le tensioni nelle due corde sono \$ T_1 \$ e \$ T_2 \$.

Per risolvere il problema devi effettuare la scomposizione delle forze.

Per ogni corda, scomponi la tensione in due componenti:

• verticale
  \$ T_1 \sin \theta_1 \$, \$ T_2 \sin \theta_2 \$
• orizzontale
  \$ T_1 \cos \theta_1 \$, \$ T_2 \cos \theta_2 \$

La condizione di equilibrio si trova quando le forze si bilanciano sia in verticale che in orizzontale.

• verticale
  La somma delle componenti verticali deve bilanciare il peso \$ P \$: $$T_1 \sin \theta_1 + T_2 \sin \theta_2 = P$$
• orizzontale
  La somma delle componenti orizzontali deve essere zero: $$T_1 \cos \theta_1 = T_2 \cos \theta_2$$

Adesso hai due equazioni in due incognite (\$ T_1 \$ e \$ T_2 \$).

$$ \begin{cases} T_1 \sin \theta_1 + T_2 \sin \theta_2 = P \\ \\ T_1 \cos \theta_1 = T_2 \cos \theta_2  \end{cases} $$

Le puoi risolvere con metodi classici (sostituzione o sistemi lineari).

In questo esempio sai già che $ N = 100 \ N $ , $ \theta_1 =30° $ e $ \theta_2 = 45° $.

$$ \begin{cases} T_1 \sin 30° + T_2 \sin 45° = 100 \ N \\ \\ T_1 \cos 30° = T_2 \cos 45°  \end{cases} $$

I valori delle funzioni trigonometriche sono $ \sin 30^\circ = 0.5 $, $ \cos 30^\circ \approx 0.866 $, $ \sin 45^\circ \approx 0.707 $ e $ \cos 45^\circ \approx 0.707 $

$$ \begin{cases} T_1 \cdot 0.5 + T_2 \cdot 0.855 = 100 \ N \\ \\ T_1 \cdot 0.8.666  = T_2 \cdot 0.707  \end{cases} $$

$$ \begin{cases} T_1 \cdot 0.5 + T_2 \cdot 0.855 = 100 \ N \\ \\ T_1  = T_2 \cdot \frac{ 0.707 }{ 0.8.666 } \end{cases} $$

$$ \begin{cases} T_1 \cdot 0.5 + T_2 \cdot 0.855 = 100 \ N \\ \\ T_1  = T_2 \cdot 0.816 \end{cases} $$

Ora sostituisci l’espressione di $ T_1 $ trovata sopra nella prima equazione del sistema:

$$ \begin{cases} T_2 \cdot 0.816 \cdot 0.5 + T_2 \cdot 0.855 = 100 \ N \\ \\ T_1  = T_2 \cdot 0.816 \end{cases} $$

$$ \begin{cases} T_2 \cdot (0.408+0.855) = 100 \ N \\ \\ T_1  = T_2 \cdot 0.816 \end{cases} $$

$$ \begin{cases} T_2 \cdot 1.115 = 100 \ N \\ \\ T_1  = T_2 \cdot 0.816 \end{cases} $$

$$ \begin{cases} T_2  = \frac{ 100 \ N }{ 1.115 } \\ \\ T_1  = T_2 \cdot 0.816 \end{cases} $$

$$ \begin{cases} T_2  = 89.7 \ N \\ \\ T_1  = T_2 \cdot 0.816 \end{cases} $$

Una volta trovata la tensione $ T_2 = 89.7 \ N $ sulla seconda corda, puoi sostituire questo valore nella seconda equazione.

$$ \begin{cases} T_2  = 89.7 \ N \\ \\ T_1  = ( 89.7  \ N ) \cdot 0.816 \end{cases} $$

$$ \begin{cases} T_2  = 89.7 \ N \\ \\ T_1  = 73.2 \ N \end{cases} $$

Quindi, la tensione nella prima corda è $ T_1 \approx 73.2 , \text{N} $, mentre quella nella seconda corda è $ T_2 \approx 89.7 , \text{N} $,

In conclusione, anche nelle situazioni più quotidiane, un secchio appeso, una tenda che scorre su una carrucola, un lampadario, agiscono forze in perfetto equilibrio.