Equilibrio delle forze di un corpo rigido

Un corpo rigido, a differenza di un punto materiale, può sia traslare sia ruotare.

Quando applichi una forza a un corpo esteso, il suo comportamento dipende non solo dall’intensità e dalla direzione della forza, ma anche dal punto in cui essa viene applicata.

Ricorda che un corpo rigido è un oggetto che non si deforma quando è soggetto a forze. Nella realtà, tutti gli oggetti si deformano almeno un po’, ma in molti casi possiamo trascurare queste piccole deformazioni e considerarli rigidi.

Moto di traslazione e moto di rotazione

Se le forze applicate sono bilanciate e agiscono lungo la stessa direzione, il corpo si muove con un moto di traslazione: ogni punto del corpo percorre la stessa traiettoria.

Se invece le forze non sono bilanciate o agiscono in punti diversi, il corpo può iniziare a ruotare oltre che traslare.

Esempio

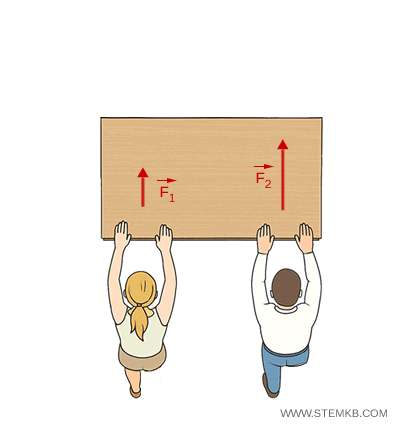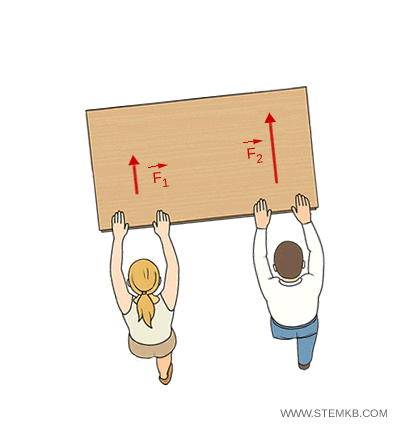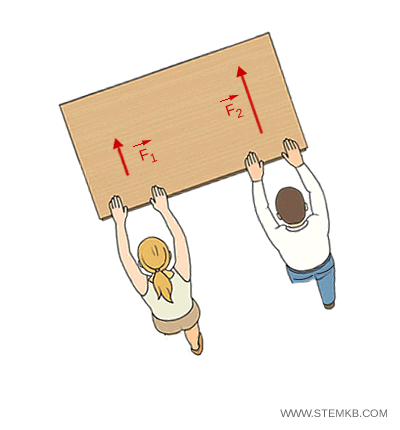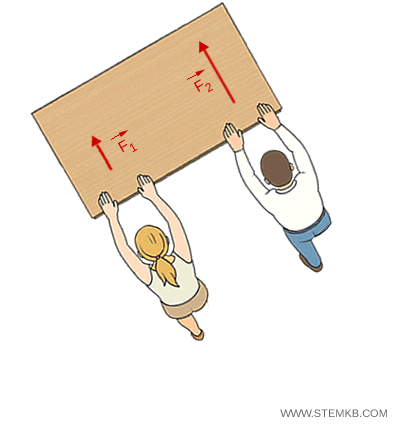
Due studenti spingono un banco. Se entrambi applicano la stessa forza in modo simmetrico, il banco si muove in avanti senza ruotare (moto traslatorio).

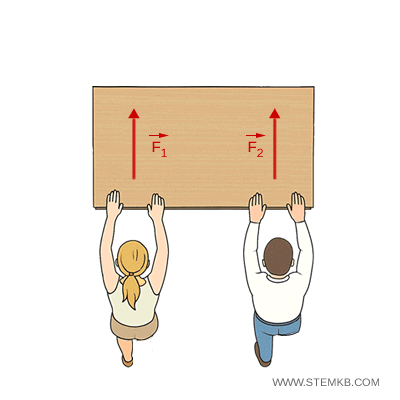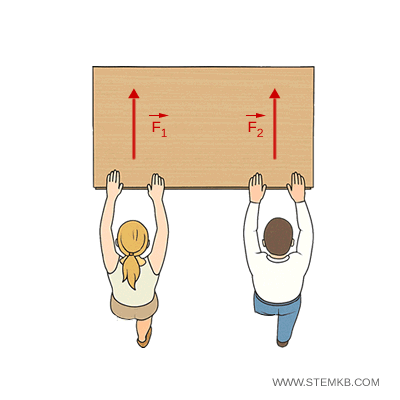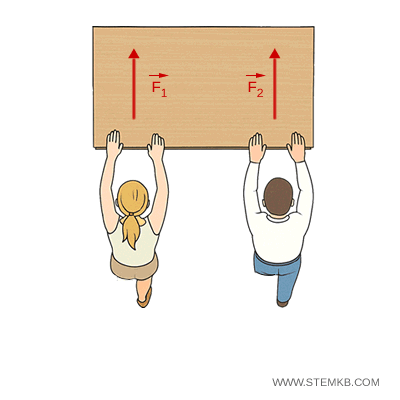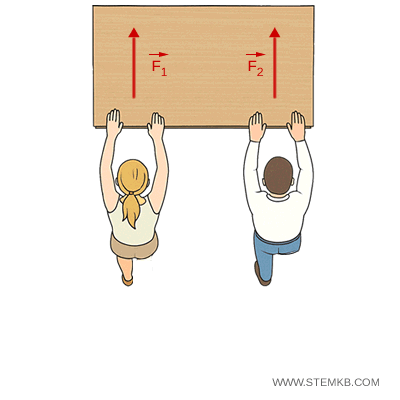
Se uno dei due applica una forza maggiore o spinge in un punto più lontano dal centro del banco, il banco oltre a traslare, ruota (moto traslatorio e rotatorio).

Il ruolo del punto di applicazione della forza

L’effetto di una forza su un corpo rigido non dipende soltanto da quanto è grande (modulo) e da come è orientata (direzione), ma anche da dove viene applicata.

Più lontano è il punto di applicazione dall’asse di rotazione, maggiore sarà l’effetto rotatorio.

Viceversa, forze applicate vicino all’asse di rotazione hanno un effetto rotatorio ridotto.

Ad esempio, mentre apri una parta se spingi vicino alle cerniere, serve molta più forza per ruotarla (F_A). Viceversa, se spingi sull’estremità opposta (lontano dall’asse), basta una forza minore (F_B) per ottenere lo stesso effetto.

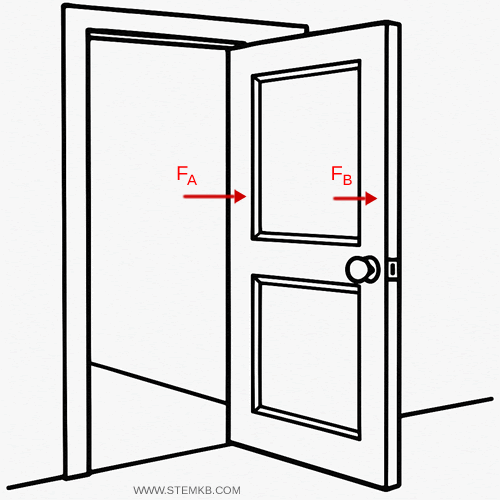
Per descrivere l’effetto rotatorio di una forza su un corpo rigido si introduce una nuova grandezza fisica: il momento torcente.

Il momento torcente dipende dal modulo della forza applicata e dalla distanza perpendicolare tra la retta d’azione della forza e l’asse di rotazione (braccio della leva)

$M = F \cdot d$

In questa formula $ M $ = momento torcente, $F$ = forza applicata, $d$ = distanza perpendicolare (braccio).

Le condizioni di equilibrio

Perché un corpo rigido sia in equilibrio devono essere soddisfatte due condizioni:

• La somma delle forze deve essere zero (nessuna accelerazione traslazionale). $$\sum F = 0$$
• La somma dei momenti torcenti deve essere zero (nessuna accelerazione angolare). $$\sum M = 0$$

Se anche una sola di queste condizioni non è rispettata, il corpo si muoverà.

Ad esempio, un libro appoggiato sul tavolo è in equilibrio perché il suo peso verso il basso è bilanciato dalla spinta verso l’alto del tavolo. Nessuna forza lo fa muovere.

La composizione delle forze su un corpo rigido

Quando più forze agiscono su un corpo rigido, è spesso necessario sostituirle con un’unica forza equivalente. Questo procedimento si chiama composizione delle forze.

1] Forze sulla stessa retta di azione

Il primo caso da considerare è quello in cui le forze hanno la stessa retta di azione.

La retta di azione è quella linea ideale lungo la quale è diretta la forza.

Quando due forze $F_1 $ e $F_2 $ agiscono sulla stessa retta di azione possono avere lo stesso verso (sono concordi) oppure verso opposto (sono discordi).

In questi casi, possiamo spostare le forze lungo la retta in modo da far coincidere i punti di applicazione $ P $, senza cambiare il suo effetto complessivo.

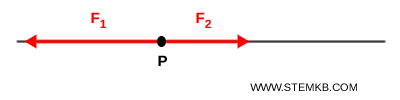
Questo principio semplifica molto i calcoli nei ei problemi di meccanica..

Poi si sommano algebricamente i loro valori (moduli), tenendo conto dei versi.

• Se le due forze hanno lo stesso verso si sommano $$ F_R = F_1 + F_2$$
• Se hanno il verso opposto si calcola la differenza assoluta e il verso della risultanteè quello della forza più grande. $$F_R = |F_1 - F_2|$$

Esempio

Immaginiamo di spingere una cassa lungo la stessa la inea di azione.

La prima forza è $F_1 = 10 \ N $ verso destra mentre la seconda è $F_2 = 6 N $ verso sinistra.

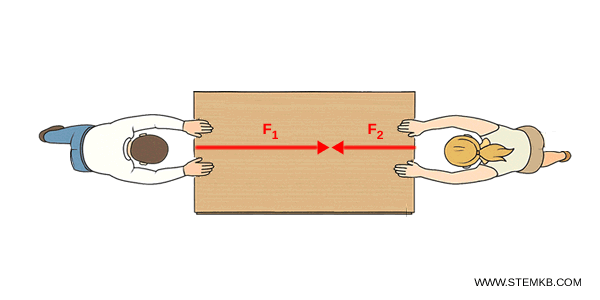
Spostiamo una forza, ad esempio la $ F_2 $, sullo stesso punto di applicazione dell'altra.

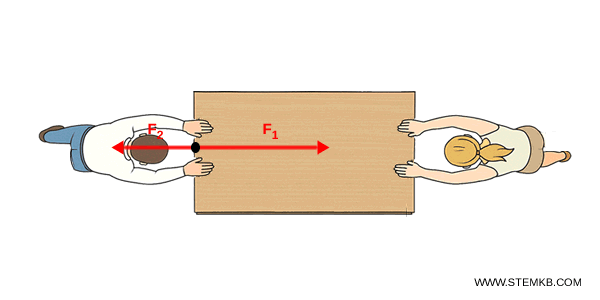
Poi le sommiamo algebricamente.

Poiché le forze sono sulla stessa retta ma di verso opposto, calcolo la forza risultante:

$$ F_R = |10\,\text{N} - 6\,\text{N}| = 4\,\text{N} $$

In pratica, la cassa sarà spinta verso destra da una forza risultante netta di 4 N.

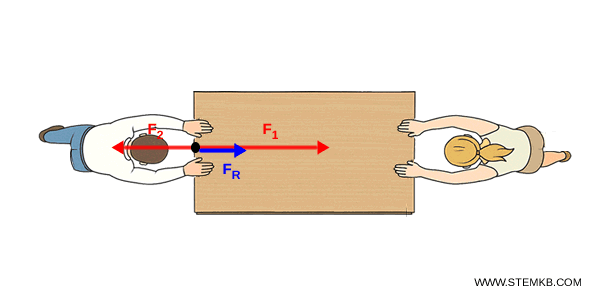
Si sposta verso destra perché è il verso della forza più grande $ F_1 > F_2 $..

Se, invece, entrambe le forze fossero dirette verso destra (concordi), la forza risultante sarebbe: $$ F_R = 10\,\text{N} + 6\,\text{N} = 16\,\text{N} $$ Quindi il carrello sarebbe spinto verso destra da una forza maggiore.

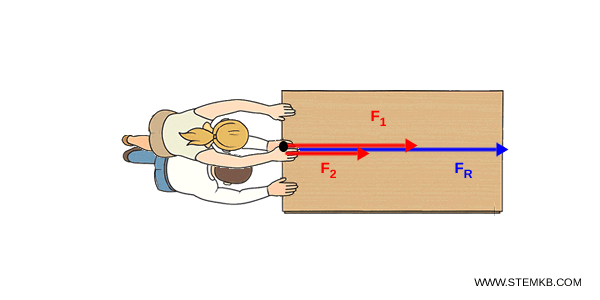
E' il primo passo per capire casi più complessi, come le forze concorrenti o parallele.

2] Forze parallele e concordi

Due forze si dicono parallele e concordi quando hanno rette d’azione parallele, cioè sono orientate nella stessa direzione, e hanno lo stesso verso.

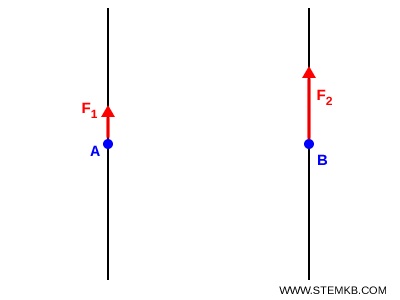
Se consideri due forze $F_1$ e $F_2$, applicate nei punti A e B, la loro forza risultante $F_R$ ha la stessa direzione e verso delle due forze e ha come intensità la somma delle due intensità:

$$ F_R = F_1 + F_2 $$

La forza risultante non si applica né esattamente in A né in B, ma in un punto intermedio $C$ sul segmento $AB$ che congiunge i due punti.

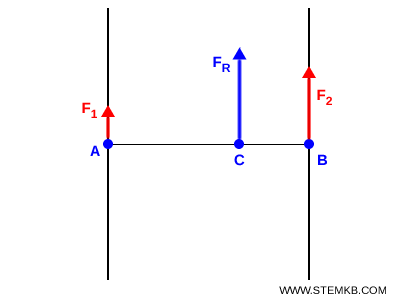
Il punto $C$ divide il segmento $AB$ in due parti, $AC$ e $CB$, in modo inversamente proporzionale alle intensità delle due forze:

$$ AC : CB = F_2 : F_1 $$

In altre parole, il punto di applicazione della risultante si sposta verso la forza più intensa,

Ad esempio, se $F_1$ è più grande di $F_2$, il punto $C$ sarà più vicino a $A$. Viceversa, se $F_2$ è più grande di $F_1$, il punto $C$ sarà più vicino a $B$.

Esempio

Due persone spingono una cassa in due punti diversi con forze parallele e concordi.

Una persona spinge nel punto $ A $ con una forza $ F_1 = 10 \ N $ mentre l'altra spinge nel punto $ B $ con una forza $ F_2 = 30 \ N $.

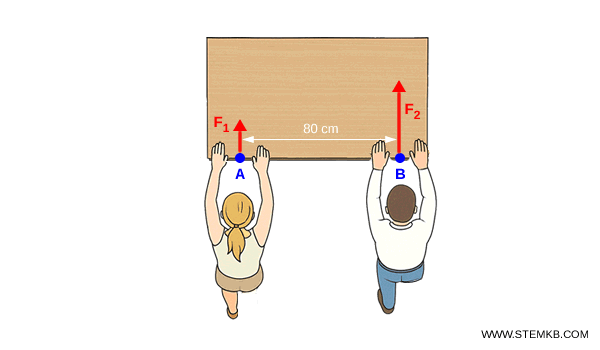
La distanza tra $A$ e $B$ è: $AB = 80\, \text{cm}$

Per prima cosa devi calcolare la somma risultante facendo la somma algebrica delle forze.

$$ F_R = F_1 + F_2 = 10 + 30 = 40\, \text{N} $$

Poi devi trovare la posizione del punto di applicazione $C$ della forza risultante $ F_R $.

$$ AC : CB = F_2 : F_1 $$

Sostituisci le intensità delle forze $ F_1 = 10 \ N $ e $ F_2 = 30 \ N $

$$ AC : CB = 30 : 10 $$

Significa che su un totale di 30 + 10 = 40 parti

• il segmento AC occupa 30 parti su 40 di $ AC+CB $
• il segmento CB occupa 10 parti su 40 di $ AC+CB $

Quindi puoi ricavare la lunghezza del segmento AC in questo modo:

$$ AC = \frac{30}{40} \times (AC+CB) $$

ossia

$$ AC = \frac{3}{4} \times (AC+CB) $$

Siccome $AC + CB = AB = 80\, \text{cm}$, puoi scrivere:

$$ AC = \frac{3}{4} \times 80 \ cm = 60 \ cm  $$

Quindi, la forza risultante $F_R = 40\, \text{N}$ si applica nel punto $C$, a 60 cm da A e 20 cm da B.

Essendo $F_2$ la forza più grande, il punto $C$ è più vicino a $B$.

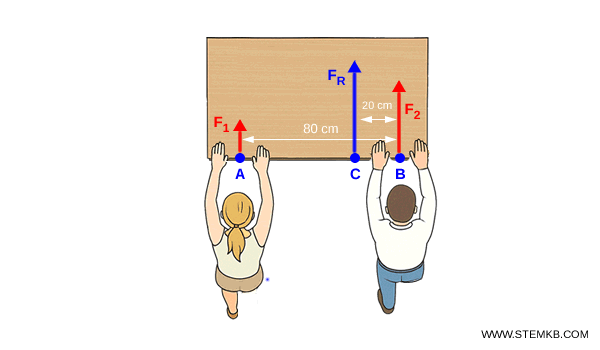
In altre parole, è come se una sola persona spingesse la cassa nel punto $ C $ con una forza $ F_R = 40 \ N $.

3] Forze parallele e discordi

Due forze che agiscono su un corpo rigido si dicono parallele e discordi quando hanno la stessa direzione ma le loro linee d'azione sono parallele e hanno versi opposti.

Queste forze possono avere intensità diverse e i loro punti di applicazione non coincidono.

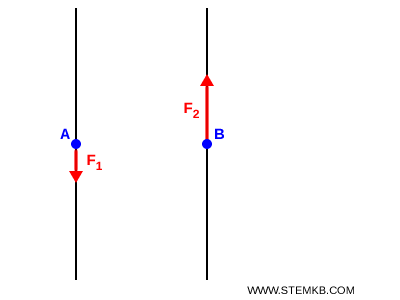
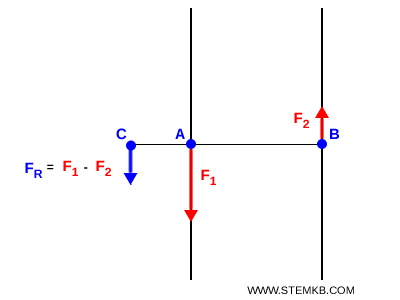
Se consideri due forze $F_1$ e $F_2$, applicate nei punti $ A $ e $ B $, la loro forza risultante $F_R$ ha la stessa direzione e si calcola sottraendo la forza minore da quella maggiore:

$$ F_R = \begin{cases} F_1 - F_2 \ \ \ \ se \ \ \ F_1 \ge F_2 \\ \\ F_2 - F_1 \ \ \ \ se \ \ \ F_2 > F_1 \end{cases} $$

In alternativa, puoi calcolarla anche come valore assoluto della differenza tra le due forze:

$$ F_R = | F_1 - F_2 | $$

Quindi la forza risultante $ F_R $ ha la stessa direzione delle due forze, il verso della forza di intensità maggiore e l'intensità pari alla differenza assoluta tra le due forze.

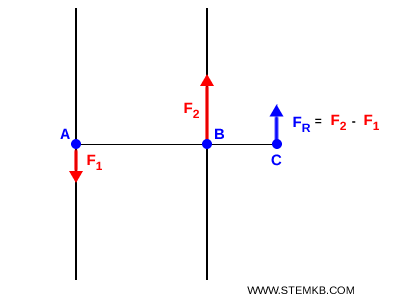
Il punto di applicazione $ C $ della forza risultante si trova sul prolungamento del segmento $AB$ che unisce i punti di applicazione delle due forze $A$ e $B$  dalla parte della forza maggiore, in modo tale che i due segmenti  $AC$ e $BC$ siano tra loro in proporzione inversa a quella di $ F_1 $ e $ F_2 $

$$ AC : BC = F_2 : F_1 $$

In altre parole, la distanza del punto $ A $ dal punto $ C $, moltiplicata per la forza $ F_1 $ applicata in $ A $, deve essere uguale alla distanza del punto $ B $ da $ C $, moltiplicata per la forza $ F_2 $ applicata in $ B $.

$$ AC \times F_1 = BC \times F_2 $$

La proporzione è sempre la stessa. Cambiano solo chi è la forza maggiore e da che parte sta il punto C.

Ad esempio, se $ F_1 > F_2 $ il punto di applicazione $ C $ si troverebbe dalla parte del punto $ A $. La proporzione $ AC : BC = F_2 : F_1 $ resta comunque la stessa.

Esempio

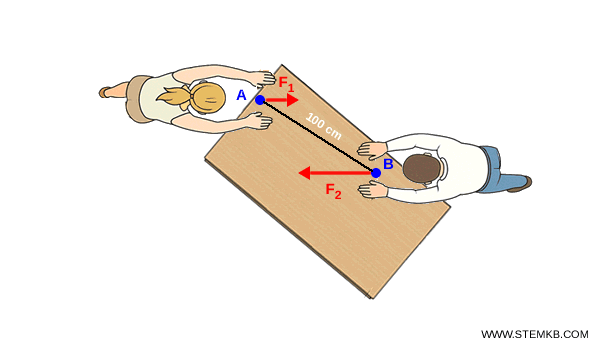
Facciamo un esempio pratico, due persone spingono una cassa in due punti diversi $ A $ e $ B $ rispettivamente con le seguenti forze parallele e discordi: $F_1 = 10 \ N $ verso destra e $F_2 = 30 \ N  $ verso sinistra

Il segmento $ AB $ che unisce i due punti di applicazione è lungo $ 100 \ cm $.

In questo caso $ F_2 > F_1 $ quindi la risultante delle forze sarà:

$$ F_R = F_2 - F_1 = 30 \, \text{N} - 10 \, \text{N} = 20 \, \text{N} $$

Questa forza risultante ha verso sinistra, come $F_2$, e agisce in un punto preciso che chiamiamo $C$.

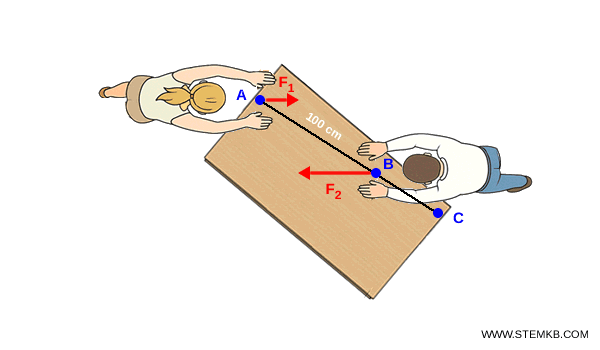
Il punto $C$ si trova sul prolungamento del segmento $ AB $ dalla parte di $ B $, poiché $ F_2 $ è la forza maggiore, e soddisfa la seguente proporzione

$$ \frac{AC}{BC} = \frac{F_2}{F_1} $$

In altre parole, le due parti $ AC $ e $ BC $ sono in proporzione inversa rispetto alle forze.​

Sostituisci i valori delle forze $ F_1 = 10 \ N $ e $ F_2 = 30 \ N $

$$ \frac{AC}{BC} = \frac{30}{10} $$

ossia

$$ \frac{AC}{BC} = 3 $$

Poiché $ AC = AB + BC $ e  $ AB = 100 \ cm $ allora $ AC = 100 \ cm + BC $

$$ \frac{100 \ cm + BC}{BC} =3 $$

Moltiplica in croce e ottieni:

$$ 100 \ cm + BC = 3BC $$

Ora ricava la lunghezza del prolungamento $ BC $

$$ 3BC - BC = 100 \ cm $$

$$ 2BC = 100 \ cm $$

$$ BC = \frac{100 \ cm}{2} = 50 \ cm $$

Questo significa che il punto $ C $ si trova a $ 50 cm $ oltre $ B $, sul prolungamento dalla parte della forza maggiore $ F_2 $​.

La forza risultante $ F_R $ si considera applicata nel punto $ C $, detto punto di applicazione equivalente, con intensità 20 N verso sinistra.

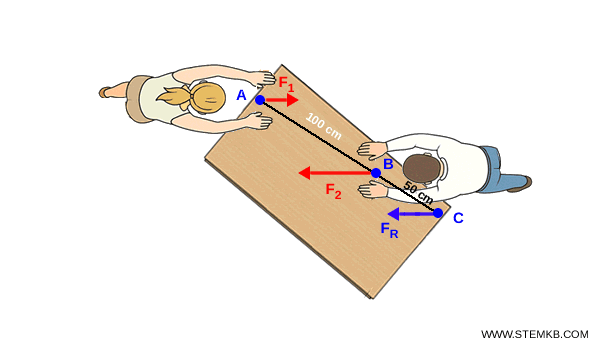
In conclusione, l’azione di due forze parallele e discordi produce una forza risultante (traslazione del corpo) e un momento risultante se le forze non sono applicate sulla stessa linea, il che può generare rotazione del corpo.

Se le due forze hanno intensità uguale, la loro risultante è nulla, ma producono una coppia di forze, ossia un sistema di forze con somma nulla ma con momento risultante diverso da zero, capace di far ruotare il corpo rigido senza spostarlo. Ad esempio, se $F_1 = F_2 = 15 \, \text{N}$, le forze si annullano come forza risultante, ma il corpo può ruotare perché le due forze formano una coppia.

4] Forze concorrenti

Due forze $ F_1 $ e $ F_2 $ si dicono concorrenti quando agiscono su punti distinti $ A $ e $ B $ di un corpo rigido, ma le loro rette di azione si intersecano in un unico punto $ C $.

Questo punto di intersezione può trovarsi sia dentro, sia fuori dal corpo rigido. Quindi, non è un errore se il punto di intersezione è esterno: è una situazione assolutamente normale nella meccanica dei corpi rigidi.

Come si compongono due forze concorrenti?

Per calcolare la forza risultante devi procedere in questo modo:

1. Traccia le rette di azione delle due forze concorrenti $ F_1 $ e $ F_2 $
   
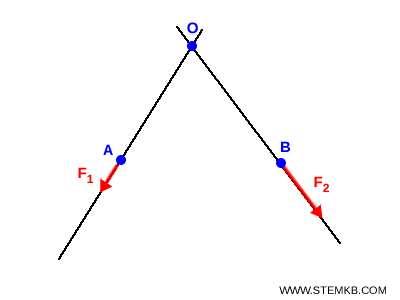
2. Sposta le due forze lungo le loro rette di azione fino a farle passare per il punto di intersezione $ O $. Ricorda che una forza è un vettore applicato lungo una retta di azione, quindi puoi spostarla su quella retta senza modificarne l’effetto meccanico sul corpo rigido.
   
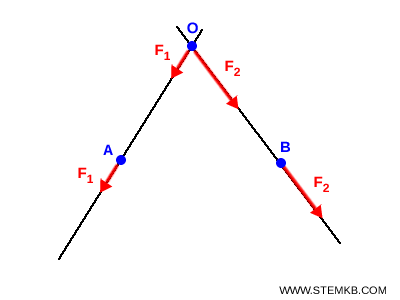
3. Utilizza il metodo del parallelogramma o il metodo punta-coda per sommare i due vettori delle forze. In questo modo ottieni la forza risultante $ F_R $.
   
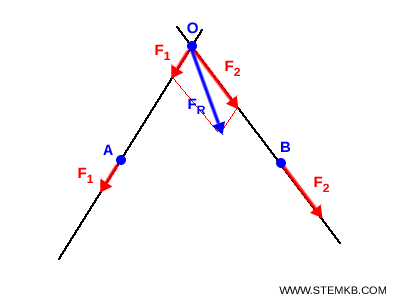
4. Traccia la retta di azione della forza risultante $ F_R $. Poi sposta la risultante lungo la sua retta di azione fino al punto $ C $, ossia il punto di intersezione tra la retta di azione della risultante e il segmento $AB$ che unisce i punti di applicazione $A$ e $B$ delle due forze originali.
   

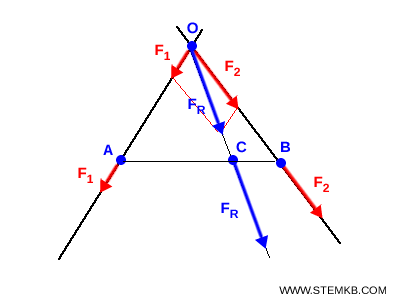
Questo passaggio è fondamentale perché ti consente di sapere dove applicare la forza risultante in modo da produrre sul corpo rigido lo stesso effetto complessivo delle due forze originali.

Esempio

Considera due forze:

• $ F_1 $ = 8 N applicata nel punto $A$, diretta verso destra.
• $ F_2 $ = 10 N applicata nel punto $B$, inclinata di 30° rispetto a $ F_1 $.

Supponi che le rette di azione delle due forze si incontrino in un punto $ O $ fuori dal corpo rigido.

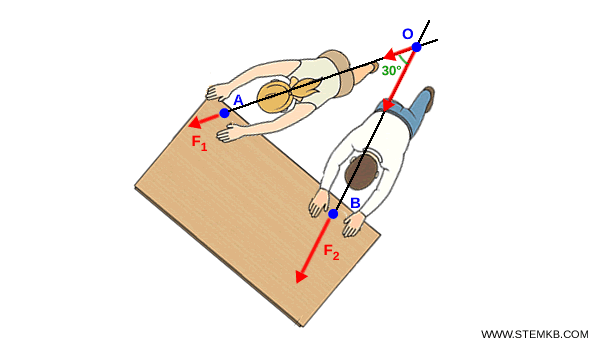
Trasla i vettori $ F_1 $ e $ F_2 $ lungo le rispettive rette di azione fino al punto $ O $.

Poi calcola il vettore della forza risultante $ F_R $ usando il metodo del parallelogramma o il metodo punta-coda.

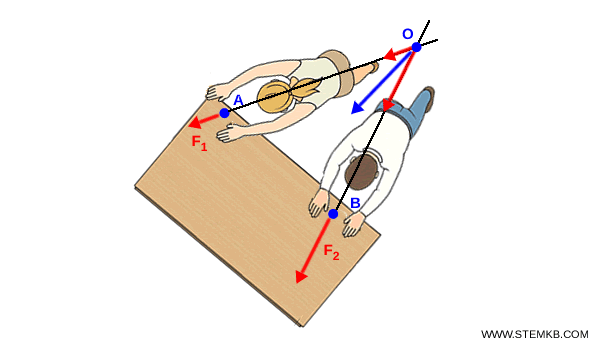
Utilizza la formula della somma vettoriale per trovare l’intensità della risultante $ F_R $:

$$ F_R = \sqrt{F_1^2 + F_2^2 + 2 \cdot F_1 \cdot F_2 \cdot \cos(30°)} $$

Sostituisci i valori:

$$ F_R = \sqrt{10^2 + 8^2 + 2 \cdot 10 \cdot 8 \cdot \frac{\sqrt{3}}{2}} = \sqrt{100 + 64 + 138.8} = \sqrt{303} \approx 17.4\,\text{N} $$

Ora traccia la retta di azione di $ F_R $ passando per $ O $.

Infine, sposta $ F_R $ lungo la sua retta di azione fino al punto $C$, ossia il punto di intersezione tra la retta di azione di $ F_R  $ e il segmento $AB$.

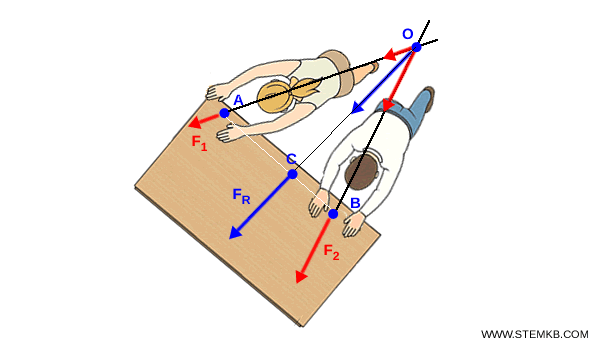
In questo modo, la forza $ F_R $ è applicata nel punto $ C $ e produce sul corpo rigido lo stesso effetto complessivo delle due forze $ F_1 $ e $ F_2 $.