Le categorie

Una categoria è una struttura che consiste di due elementi fondamentali: oggetti e morfismi (o frecce) tra questi oggetti.

In matematica è uno dei concetti fondamentali della teoria delle categorie.

Ogni categoria è caratterizzata da due componenti:

• Oggetti: Gli oggetti possono essere qualsiasi cosa, a seconda della categoria specifica. Ad esempio, possono essere insiemi, spazi, gruppi, ecc.
• Morfismi: I morfismi sono le "frecce" che collegano un oggetto a un altro. Ogni morfismo ha un oggetto di partenza e un oggetto di arrivo. I morfismi possono essere pensati come le funzioni o le trasformazioni tra oggetti.

Oltre a questi elementi, una categoria deve soddisfare anche le seguenti proprietà:

• Identità: Per ogni oggetto \( X \) nella categoria, deve esistere un morfismo identità \( id_X \) che mappa \( X \) in sé stesso. Questo morfismo deve funzionare come un elemento neutro nell'operazione di composizione, ovvero per ogni morfismo \( f : X \to Y \), deve valere \( f \circ id_X = f \) e \( id_Y \circ f = f \).
• Composizione: Deve esistere una legge di composizione per i morfismi. Se \( f \) è un morfismo da \( X \) a \( Y \) e \( g \) è un morfismo da \( Y \) a \( Z \), allora deve esistere un morfismo \( g \circ f \) da \( X \) a \( Z \). Questa operazione di composizione deve essere associativa, il che significa che se \( h \) è un morfismo da \( Z \) a un altro oggetto \( W \), allora \( h \circ (g \circ f) = (h \circ g) \circ f \).

Nonostante la sua astrazione, la teoria delle categorie si rivela una lente incredibilmente potente attraverso cui esplorare e comprendere diverse aree della matematica e, più in generale, delle scienze.

Uno degli aspetti più importanti delle categorie è proprio la loro capacità di astrazione. Partendo dal concreto, come insiemi e funzioni, la teoria delle categorie ci eleva a un livello dove possiamo parlare di oggetti e morfismi in modi che sono indipendenti dai dettagli sottostanti. Questo non solo aiuta a semplificare i problemi complessi, ma permette anche di trasferire intuizioni e risultati tra contesti e discipline scientifiche diverse. Non necessariamente solo in ambito matematico.

Esempio

Un esempio molto basilare e chiaro di categoria è la categoria degli insiemi, spesso indicata come Set.

L'insieme degli oggetti della categoria Set è composto da tre insiemi

$$ Obj(Set) = \{A, B, C \} $$

Supponiamo di avere tre insiemi finiti

$$ A = \{1, 2, 3\} $$

$$ B = \{x, y\} $$

$$ C = \{true, false\} $$

L'insieme dei morfismi della categoria Set è, invece, composto da due funzioni:

$$ Mor(Set) = \{ f. g \} $$

Come vedremo alla fine dell'esercizio, oltre questi morfismi detti "diretti", nell'insieme $ Mor(Set) $ dovremo considerare anche le composizioni dei morfismi e i morfismi identità.

Supponiamo che le funzioni siano le seguenti:

$$  f : A \to B  $$

$$ f(1) = x \\ f(2) = x \\ f(3) = y $$

$$ g : B \to C $$

$$ g(x) = true \\ g(y) = false $$

Per maggiore chiarezza possiamo rappresentare gli oggetti e i morfismi della categoria tramite i diagrammi di Eulero-Venn.

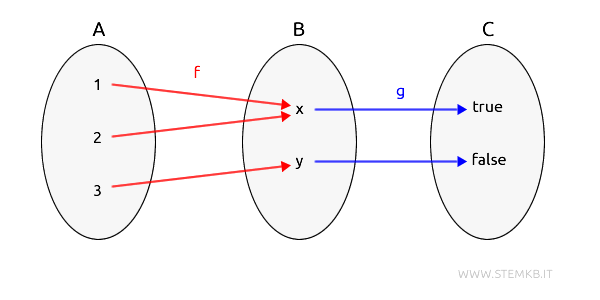
Componendo i due morfismi $ f $ e $ g $ possiamo aggiungere alla categoria una composizione di morfismo $ g \circ f $ da A a C.

$$  g \circ f : A \to C $$

$$ (g \circ f)(1) = g(f(1)) = g(x) = true \\ (g \circ f)(2) = g(f(2)) = g(x) = true \\ (g \circ f)(3) = g(f(3)) = g(y) = false $$

Oltre alle composizioni la categoria è anche composta dai morfismi identità che collegano ogni oggetto a se stesso.

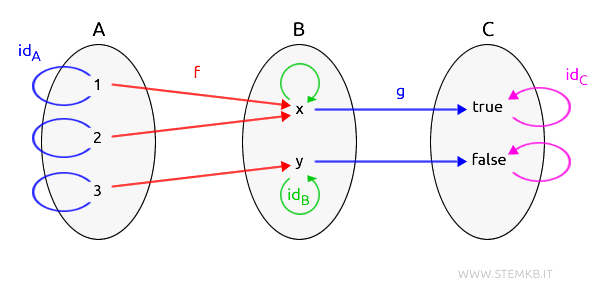
In questo caso nella categoria ci sono tre oggetti (insiemi A, B, C), quindi ci sono tre morfismi identità.

$$ id(A): A \to A $$

$$ id(B): B \to B $$

$$ id(C): B \to C $$

L'insieme di tutti i morfismi è, pertanto, composto dai morfismi diretti, dalle composizioni possibili e dai morfismi identità.

$$ Mor(Set) = \{ f. g, f \circ g, id(A), id(B), id(C) \} $$

Questo esempio illustra chiaramente come le funzioni (morfismi) e gli insiemi (oggetti) interagiscano tra loro nella categoria Set.

Tipi di categorie: piccole e grandi

In teoria delle categorie, le categorie sono distinte in "piccole" (small) e "grandi" (large) in base alla dimensione degli insiemi di oggetti e morfismi che contengono.

• Categoria piccola (Small Category)
  Una categoria piccola è una categoria in cui sia l'insieme degli oggetti Obj() sia l'insieme di tutti i morfismi Mor() sono insiemi. In altre parole, sia gli oggetti che i morfismi possono essere raccolti in un insieme che non viola le leggi della teoria degli insiemi standard.

  Ad esempio, sono esempi di categorie piccole la categoria degli insiemi finiti (FinSet) e la categoria dei gruppi finiti (Grp) e dei loro omomorfismi. Queste categorie sono "piccole" perché contengono un numero gestibile di oggetti e morfismi che possono essere espressi completamente come insiemi.

• Categoria grande (Large Category)
  Una categoria grande è una categoria in cui almeno uno tra l'insieme degli oggetti o l'insieme dei morfismi forma una classe propria, piuttosto che un insieme. Questo significa che l'insieme degli oggetti o dei morfismi è troppo grande per essere gestito all'interno dei vincoli normali della teoria degli insiemi, come accade con le categorie che includono, ad esempio, tutti gli insiemi possibili o tutti gli spazi topologici.

  Ad esempio, la categoria di tutti gli insiemi (Set) con funzioni come morfismo è considerata una grande categoria, perché l'insieme di tutti gli insiemi non è un insieme secondo le regole della teoria degli insiemi e non evita paradossi come il paradosso di Russell.

La distinzione tra categorie piccole e grandi è importante perché le categorie grandi possono presentare sfide uniche in termini di manipolazione matematica e logica. Gli strumenti usati per gestire classi proprie sono molto più sofisticati e spesso richiedono cautele aggiuntive, come l'uso di universi in alcuni approcci alla teoria delle categorie.