Il morfismo identità nella teoria delle categorie
Nella teoria delle categorie, il morfismo identità su un oggetto $ A $ mappa ogni elemento di \( A \) su se stesso. Viene indicato con $ \text{id}_A $ oppure con $ 1_A $. $$ \forall \ a \ \in A \ , \ \text{id}_A(a) = a $$
Per ogni oggetto \( A \) in una categoria, esiste un morfismo identità \( \text{id}_A : A \to A \) che soddisfa le seguenti proprietà:
- Identità
Il morfismo identità su \( A \), \( \text{id}_A \), è un morfismo che mappa ogni elemento di \( A \) su se stesso. - Composizione di morfismi
Per qualsiasi morfismo \( f: A \to B \) e qualsiasi morfismo \( g: B \to A \), la composizione di \( f \) con \( \text{id}_A \) e di \( \text{id}_B \) con \( f \) restituisce \( f \) stesso, cioè $$ f \circ \text{id}_A = f $$ $$ \text{id}_B \circ f = f $$ Questo mostra che \( \text{id}_A \) e \( \text{id}_B \) agiscono come elementi neutri per la composizione di morfismi.
Il morfismo identità è quindi essenziale per mantenere l'integrità degli oggetti all'interno della categoria, assicurando che la composizione di morfismi sia ben definita e che la categoria sia chiusa rispetto a questa operazione.
Esempio
Facciamo un esempio pratico di categoria e di morfismo identità per vedere concretamente come funziona.
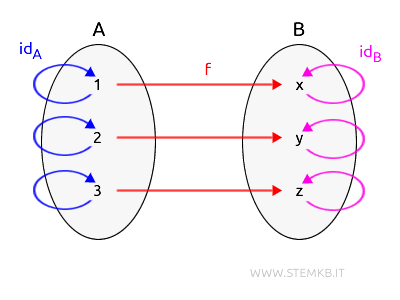
Prendiamo una categoria chiamata Set che contiene due oggetti e un morfismo (funzione)
$$ Obj(Set) = \{ A, B \} $$
Gli oggetti sono due insiemi finiti A e B.
$$ A = \{1, 2, 3\} $$
$$ B = \{x, y, z\} $$
La categoria Set include anche un solo morfismo f.
$$ Mor(Set) = \{ f , g \} $$
La funzione \( f: A \rightarrow B \) è una funzione definita come segue:
$$ f(1) = x $$
$$ f(2) = y $$
$$ f(3) = z $$
Per definizione ogni oggetto della categoria Set ha un morfismo identità che mappa ogni elemento su se stesso.
Il morfismo identità su $ A $ e il morfismo identità su $ B $
$$ \text{id}_A: A \rightarrow A $$
$$ \text{id}_B: B \rightarrow B $$
Ora consideriamo la composizione di \( f \) con \( \text{id}_A \)
$$ f \circ \text{id}_A: A \rightarrow B $$
Questa composizione significa applicare prima \( \text{id}_A \) e poi \( f \).
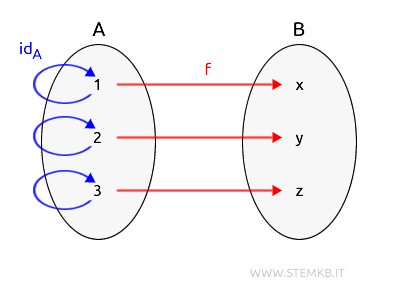
Dal momento che \( \text{id}_A \) non cambia gli elementi di \( A \), \( f \circ \text{id}_A \) sarà effettivamente uguale a \( f \).
$$ f \circ \text{id}_A(1) = f(1) = x $$
$$ f \circ \text{id}_A(2) = f(2) = y $$
$$ f \circ \text{id}_A(3) = f(3) = z $$
Allo stesso modo la composizione di \( \text{id}_B \) con \( f \) produce lo stesso risultato:
$$ \text{id}_B \circ f: A \rightarrow B $$
Questa composizione applica prima \( f \) e poi \( \text{id}_B \).
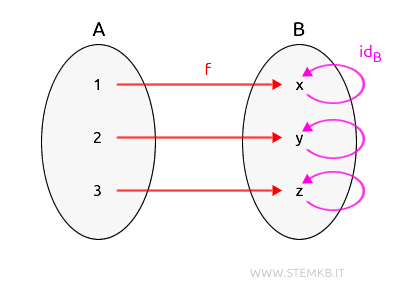
Dato che \( \text{id}_B \) non modifica gli elementi di \( B \), \( \text{id}_B \circ f \) sarà anch'esso uguale a \( f \).
$$ \text{id}_B \circ f(1) = \text{id}_B(x) = x $$
$$ \text{id}_B \circ f(2) = \text{id}_B(y) = y $$
$$ \text{id}_B \circ f(3) = \text{id}_B(z) = z $$
In entrambi i casi, la composizione di \( f \) con i morfismi identità \( \text{id}_A \) o \( \text{id}_B \) non altera il comportamento di \( f \), confermando che \( \text{id}_A \) e \( \text{id}_B \) agiscono come elementi neutri nella composizione delle funzioni.
Questo esempio mostra chiaramente come i morfismi identità permettono di preservare le operazioni tra oggetti nella teoria delle categorie.