I morfismi nella teoria delle categorie

Nella teoria delle categorie un morfismo è una funzione che collega un oggetto A (detto dominio) e un altro oggetto B (detto codominio) all'interno di una stessa categoria. $$ f: A \rightarrow B $$ E' anche detto freccia o mappa. Spesso è indicato anche con $ f_{AB} $.

I morfismi possono essere concepiti come funzioni che collegano gli oggetti all'interno di una categoria, dove tali oggetti possono essere qualsiasi entità matematica.

Ad esempio, tra gli oggetti rientrano insiemi, spazi vettoriali, gruppi, ecc.

I morfismi in una categoria sono essenziali per definire la struttura e le relazioni tra gli oggetti. Permettono di esprimere processi, funzioni e trasformazioni in un modo che è coerente all'interno della struttura matematica della categoria.

Ogni morfismo è sempre caratterizzato da un oggetto di partenza (dominio) e da un oggetto di arrivo (codominio) che non necessariamente sono diversi.

$$ f: \underbrace{A}_{\text{dominio}} \rightarrow \underbrace{B}_{\text{codominio}} $$

Inoltre, ha sempre un verso. Quindi i morfismi $ f_{AB} $ e $ f_{BA} $ sono due morfismi distinti tra gli stessi oggetti.

Le proprietà dei morfismi

I morfismi devono soddisfare tre condizioni essenziali:

• Ogni morfismo ha un oggetto di partenza e un oggetto di arrivo
  Ogni morfismo è una freccia che parte da un oggetto di partenza chiamato "dominio" e arriva a un oggetto di arrivo chiamato "codominio". Quindi, un morfismo ha sempre un oggetto di partenza e un oggetto di destinazione. $$ f: \underbrace{A}_{\text{dom(f)}} \rightarrow \underbrace{B}_{\text{cod(f)}} $$
• Composizione di morfismi
  Quando hai due morfismi $ f \in hom(A,B) $ e $ g \in hom(B,C) $ in cui il codominio del primo è il dominio del secondo, puoi comporli per ottenere un nuovo morfismo. $$ f ∘ g  \in hom(A,C) $$
  

  Se esiste un morfismo da A a B (f: A → B) e un morfismo da B a C (g: B → C), allora deve esistere un morfismo da A a C (g ∘ f: A → C) ottenuto componendo f e g. La composizione di morfismi soddisfa la proprietà associativa, il che significa che la maniera in cui i morfismi sono raggruppati durante la composizione non cambia il risultato. $$ f ∘ (g∘h) = (f∘g)∘h  $$

• Morfismi identità
  Ogni oggetto ha un morfismo identità che "punta" all'oggetto stesso $ 1A \in hom(A,A) $. Questo morfismo serve come elemento neutro nella composizione, cioè, quando viene composto con qualsiasi altro morfismo applicabile, il risultato è il morfismo originale.
  

  Per ogni oggetto A, esiste un morfismo identità (1A: A → A) che serve come elemento neutro per la composizione. Ciò significa che la composizione di un morfismo identità con qualsiasi altro morfismo lascia quest'ultimo invariato.

I morfismi sono quindi il "collante" che struttura la categoria, e il modo in cui interagiscono (tramite la composizione) e si relazionano con gli oggetti (tramite i domini e codomini) è ciò che dà forma alle proprietà matematiche di interesse in una categoria.

L'insieme di tutti morfismi tra due oggetti $ A $ e $ B $ in una stessa categoria è detto hom-sets ed è indicato con hom(A,B).

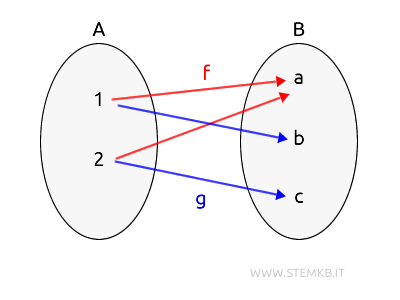
Va sottolineato che hom(A,B) include tutti i morfismi tra due oggetti specifici A e B della categoria, in particolar modo quelli da A a B, e non va confuso con l'insieme di tutti i morfismi della categoria.

L'insieme di tutti i morfismi in una categoria è un altro insieme (o classe) ed è indicato con Mor(C) dove C è la categoria in questione.

Esempio

Immaginiamo di avere una categoria semplice chiamata "Set", dove gli oggetti sono insiemi e i morfismi sono le funzioni tra insiemi.

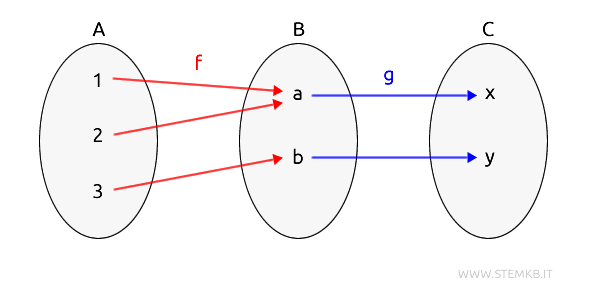
In questa categoria ci sono tre oggetti e due morfismi diretti.

• Oggetti
  Siano A = {1,2,3}, B = {a,b} e C={x,y} tre oggetti della categoria Set. $$ Obj(Set) = \{ A,B,D \} $$ Dove Set è la categoria.
• Morfismi tra oggetti
  Nella categoria ci sono due morfismi (funzioni) $$ Mor(Set) = \{f,g \}  $$
  1. La funzione \( f: A \rightarrow B \) definita come segue:
         \( f(1) = a \)
         \( f(2) = a \)
         \( f(3) = b \)
     Questa funzione \( f \) è un morfismo dall'oggetto A all'oggetto B nella categoria Set perché associa ogni elemento di A a un elemento di B.
  2. La funzione $ g: B \rightarrow C $ definita in questo modo:
          \( g(a) = x \)
          \( g(b) = y \)  
     Quest'altra funzione $ g $ è un morfismo dall'oggetto B all'oggetto C sempre nella categoria Set.
• Composizione di morfismi
  In questo esempio c'è una sola composizione possibile di morfismi. Possiamo comporre \( f \) e \( g \) per ottenere un morfismo \( g \circ f: A \rightarrow C \):
       \( g(f(1)) = g(a) = x \)
       \( g(f(2)) = g(a) = x \)
       \( g(f(3)) = g(b) = y \)  
• Morfismi identità
  Ogni insieme ha un morfismo identità. Per l'insieme A, abbiamo \( 1_A: A \rightarrow A \) dove ogni elemento di A è mappato a se stesso. Lo stesso vale per B con il morfismo identità \( 1_B: B \rightarrow B \) e per l'insieme C \( 1_C: C \rightarrow C \).

In questa categoria, quindi, le funzioni tra insiemi agiscono come morfismi, e le proprietà di composizione e identità riflettono le regole familiari che conosciamo dalle funzioni in matematica.

L'insieme di tutti i morfismi per una coppia specifica di insiemi, ad esempio da A a B, è chiamato hom-set ed è indicato come hom(A, B).

$$ hom(A,B) = \{ f \} $$

$$ hom(B,C) = \{ g \} $$

$$ \hom(A,C) = \{ g \circ f \} $$

L'insieme di tutti i morfismi Mor(Set) include, invece, tutte le possibili funzioni tra qualsiasi coppia di insiemi della categoria, le identità e le eventuali composizioni di morfismi.

$$ Mor(Set) = \{ f, g, g \circ f, 1_A, 1_B, 1_C \} $$

Questo esempio pratico illustra in modo chiaro come funzionano i morfismi e offre una panoramica completa sulle principali caratteristiche dei morfismi di una categoria.