Hom-Sets: Insiemi di morfismi nella teoria delle categorie

Un insieme di tutti i morfismi che hanno un oggetto A come dominio e un oggetto B come codominio è indicato con hom(A, B), detto insieme-morfismo o hom-sets. $$ \text{hom}(A,B) $$

L'insieme hom(A, B) in una categoria comprende solo i morfismi che vanno da A a B.

Quindi, non include i morfismi che vanno da B ad A. Questi ultimi fanno parte di un insieme di morfismi differente, indicato come hom(B, A).

Inoltre, a meno che non si stia parlando dello stesso dominio e codominio, gli insiemi dei morfismi sono distinti.

In altre parole, un morfismo specifico appartiene solo a un insieme di morfismi tra un dato dominio e codominio. Quindi, gli insiemi-morfismo sono disgiunti a meno che i loro oggetti corrispondenti non siano identici. Ad esempio, hom(A, B) e hom(C, D) sono disgiunti a meno che A non sia C e B non sia D.

Quando due morfismi appartengono allo stesso hom-set tra due oggetti \( A \) e \( B \) in una categoria sono detti "morfismi paralleli" 

Questo significa che entrambi i morfismi hanno lo stesso oggetto di partenza \( A \) e lo stesso oggetto di arrivo \( B \).

In sostanza, sono entrambi elementi dell'insieme dei morfismi che mappano \( A \) in \( B \).

L'attributo "parallelo" non implica alcuna altra relazione specifica tra i morfismi, come essere uguali o differire per qualche proprietà, ma solamente che condividono gli stessi oggetti di partenza e di arrivo nella struttura della categoria. Inoltre, non si riferisce al fatto che appartengano allo stesso "morfismo" specifico \( f_{AB} \) tra \( A \) e \( B \), poiché \( f_{AB} \) sarebbe un esempio di un singolo morfismo all'interno dell'hom-set \( \text{Hom}(A, B) \).

Esempio

Facciamo un esempio pratico di Hom-Sets nella categoria degli insiemi.

Consideriamo due insiemi finiti \( A \) e \( B \)

$$ A = \{1, 2\} $$

$$ B = \{a, b, c\} $$

L'Hom-Set \( \text{Hom}(A, B) \) comprende tutte le possibili funzioni da \( A \) a \( B \).

Ogni funzione deve assegnare un elemento di \( B \) a ciascun elemento di \( A \).

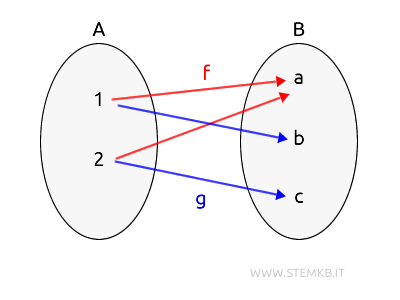
Ecco qualche esempio concreto di funzioni  che potrebbero appartenere alla classe \( \text{Hom}(A, B) \):

• Una possibile funzione \( f \) potrebbe essere quella che associa 1→a e 2→a:
    \( f(1) = a \)
    \( f(2) = a \)
• Un'altra possibile funzione \( g \) potrebbe associare 1→b e 2→c
    \( g(1) = b \)
    \( g(2) = c \)
• Un'ulteriore funzione \( h \) potrebbe associare 1→a e 2→b:
    \( h(1) = a \)
    \( h(2) = b \)

Poiché ci sono 3 scelte possibili per \( f(1) \) e 3 scelte possibili per \( f(2) \), potrebbero esserci al massimo \( 3 \times 3 = 9 \) funzioni diverse da \( A \) a \( B \).

Queste funzioni formano l'hom-set \( \text{Hom}(A, B)  \), che contiene tutti questi possibili morfismi dall'oggetto $ A $ all'oggetto $ B $.

Questo semplice esempio tra due insiemi finiti mostra come l'hom-set non sia un singolo morfismo, ma un insieme di tutti i morfismi possibili che mappano gli elementi di \( A \) agli elementi di \( B \) secondo le regole di una funzione.