Gli oggetti nella teoria delle categorie

Nella teoria delle categorie gli oggetti sono i nodi fondamentali che, insieme ai morfismi, compongono una categoria.

In generale un oggetto è un'entità astratta che può essere pensata come un punto in uno spazio.

La teoria non specifica nulla sulla struttura interna degli oggetti; ciò che conta sono i morfismi (frecce) tra oggetti, che esprimono relazioni e funzioni.

Possono essere insiemi, spazi, gruppi, tipi, ecc., a seconda della categoria specifica in questione.

Ad esempio, nella categoria degli insiemi (Set) gli oggetti sono degli insiemi, nella categoria dei gruppi (Grp) gli oggetti sono dei gruppi, e via dicendo. 

La nozione di oggetti nella teoria delle categorie è estremamente flessibile e potente proprio perché è così astratta e consente agli oggetti di assumere il ruolo di quasi qualsiasi concetto matematico.

In altre parole, non è necessario sapere cosa sono gli oggetti per capire come si relazionano tra loro. La relazione tra gli oggetti (cioè i morfismi) è più fondamentale della natura degli oggetti stessi.

La natura di un oggetto è definita dai morfismi che entrano e escono da esso. Cioè, si capisce cosa fa un oggetto osservando come interagisce con altri oggetti attraverso i morfismi.

Puoi considerare gli oggetti come i "soggetti" delle "frasi matematiche" in cui i morfismi sono le "verbi" che descrivono le azioni o le relazioni tra questi soggetti.

Quindi, nella teoria delle categorie, gli oggetti possono esistere indipendentemente dagli altri oggetti, ma acquistano significato attraverso i loro morfismi e le relazioni con altri oggetti.

E' come se gli oggetti fossero delle stelle lontane, indipendenti tra loro, che viste dalla Terra ci consentono di tracciare quelle linee immaginarie che chiamiamo "costellazioni".

La teoria delle categorie offre una nuova prospettiva che inverte il modo tradizionale di pensare: non cominci con l'oggetto e poi cerchi le funzioni, ma piuttosto cominci con le "funzioni" (morfismi) e poi scopri la natura degli oggetti dalle relazioni. Questa astrazione permette una unificazione di concetti che, altrimenti, potrebbero sembrare completamente disgiunti. Ad esempio, il concetto di oggetti in categorie diverse ma con morfismi simili (come gruppi e spazi vettoriali) consente di formulare idee come i funtori, che sono strumenti utili per trovare e studiare simmetrie e analogie profonde tra diverse aree della matematica. Quindi, questa astrazione non solo fornisce un linguaggio comune per diverse strutture matematiche, ma facilita anche la scoperta di connessioni profonde e fondamentali tra di campi diversi del sapere.

In genere gli oggetti sono rappresentati in un diagramma (grafo orientato o digrafo) come dei nodi mentre i morfismi come gli archi che collegano i nodi tra loro.

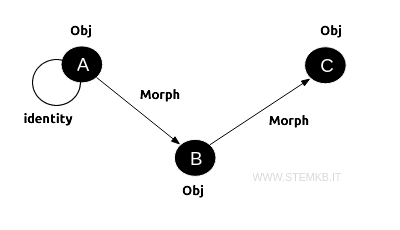
Nel complesso il diagramma è la categoria di cui fanno parte sia gli oggetti che i morfismi.

Qual è la differenza tra oggetti e categoria? Gli oggetti sono i componenti base di una categoria, mentre la categoria stessa fornisce le regole e le strutture che governano come questi oggetti possono interagire tra loro.

Inoltre, ogni oggetto ha un morfismo identità associato a esso. Questo morfismo va dall'oggetto a se stesso e serve come elemento neutro per la composizione dei morfismi.

Nel diagramma il morfismo identità è un loop, ossia un arco che collega direttamente un nodo a se stesso.

Alcuni esempi di oggetti

Ecco alcuni esempi di oggetti in diverse categorie matematiche:

• Categoria degli Insiemi (Set): Gli oggetti sono insiemi. Ad esempio, l'insieme dei numeri naturali \( \mathbb{N} \), l'insieme dei numeri reali \( \mathbb{R} \), o anche l'insieme vuoto \( \emptyset \).
• Categoria degli Spazi Vettoriali (Vect_k su un campo k): Gli oggetti sono spazi vettoriali su un campo fisso \( k \). Ad esempio, \( \mathbb{R}^2 \) e \( \mathbb{R}^3 \) sono oggetti in questa categoria, dove \( \mathbb{R} \) indica il campo dei numeri reali.
• Categoria dei Gruppi (Grp): Gli oggetti sono gruppi. Un esempio potrebbe essere il gruppo ciclico di ordine n, indicato con \( \mathbb{Z}/n\mathbb{Z} \), o il gruppo dei numeri interi sotto l'operazione di somma, indicato con \( \mathbb{Z} \).
• Categoria degli Anelli (Ring): Gli oggetti sono anelli. Ad esempio, l'anello degli interi \( \mathbb{Z} \), l'anello dei polinomi \( \mathbb{R}[x] \), o l'anello delle matrici quadrate di dimensione n su \( \mathbb{R} \), indicato con \( M_n(\mathbb{R}) \).
• Categoria delle Topologie (Top): Gli oggetti sono spazi topologici. Un esempio di oggetto in questa categoria potrebbe essere la sfera unitaria in \( \mathbb{R}^3 \), o la retta reale \( \mathbb{R} \) con la sua topologia standard.

In ogni esempio, la natura degli oggetti è definita dalla categoria a cui appartengono.

I morfismi tra questi oggetti rispettano le strutture che li caratterizzano, come le funzioni continue tra spazi topologici in Top, o gli omomorfismi di gruppo in Grp.