La composizione di morfismi
Nella teoria delle categorie una composizione di morfismi è una regola che consente di combinare due morfismi consecutivi $ f $ e $ g $ per formarne uno nuovo. $$ g \circ f $$
Consideriamo una categoria con tre oggetti $ A $, $ B $, $ C $ e due morfismi, $ f $ e $ g $
Il morfismo $ f $ va da \( A \) a \( B \)
$$ f: \ A \rightarrow B $$
Il morfismo $ g $, invece, va da \( B \) a \( C \)
$$ g: \ B \rightarrow C $$
Poiché il codominio (A) del primo morfismo corrisponde al dominio del secondo morfismo, possiamo comporre i due morfismi in un solo morfismo che scriviamo \( g \circ f \).
A volte la composizione di morfismi è scritta semplicemente come $ gf $ se non c'è rischio di confusione,
La composizione dei morfismi \( g \circ f \) è un nuovo morfismo da \( A \) a \( C \) che otteniamo applicando prima $ f $ e poi $ g $.
$$ g \circ f: \ A \rightarrow C $$
In altre parole, nella composizione \( g \circ f \), la funzione \( f \) viene applicata per prima e il risultato di \( f \) viene poi utilizzato come input per la funzione \( g \).
Le proprietà della composizione di morfismi
Ogni composizione di morfismi soddisfa le seguenti proprietà:
- Associatività: Se ci sono tre morfismi \( f: A \rightarrow B \), \( g: B \rightarrow C \), e \( h: C \rightarrow D \), allora la composizione deve soddisfare la proprietà associativa: \( (h \circ g) \circ f = h \circ (g \circ f) \). Questo significa che non importa come si raggruppano le composizioni; il risultato sarà lo stesso.
- Elemento neutro: Per ogni oggetto \( A \), esiste un morfismo identità \( 1_A: A \rightarrow A \) che funge da elemento neutro per la composizione. Questo significa che per ogni morfismo \( f: A \rightarrow B \), la composizione di \( f \) con l'identità dà \( f \circ 1_A = f \) e \( 1_B \circ f = f \).
Puoi rappresentare la composizione dei morfismi si può usare un diagramma
$$ A \rightarrow B \rightarrow C $$
Dove la freccia diretta da \( A \) a \( C \) passando attraverso \( B \) rappresenta \( g \circ f \).
Esempio
Consideriamo la categoria denominata 'Set', nella quale gli oggetti sono definiti come insiemi e i morfismi corrispondono a funzioni tra tali insiemi.
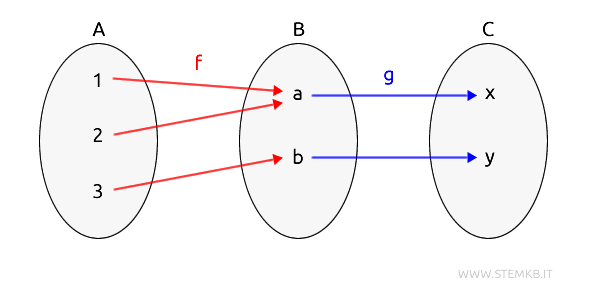
In questa categoria ci sono tre oggetti $ Obj(Set) = \{ A,B,D \} $ e due morfismi diretti $ mor(Set) = \{f,g \} $.
Il morfismo \( f: A \rightarrow B \) è definito in questo modo:
$$ f(1) = a $$
$$ f(2) = a $$
$$ f(3) = b $$
Il morfismo $ g: B \rightarrow C $ è invece il seguente:
$$ g(a) = x $$
$$ g(b) = y $$
Poiché il codominio della funzione \( f: A \rightarrow B \) coincide con il dominio della funzione $ g: B \rightarrow C $, possiamo comporre questi morfismi.
La composizione di questi due morfismi $ f $ e $ g $ è un altro morfismo $ g \circ f $ che va da $ A $ a $ C $
$$ g \circ f: A \rightarrow C $$
$$ g(f(1)) = g(a) = x $$
$$ g(f(2)) = g(a) = x $$
$$ g(f(3)) = g(b) = y $$
In conclusione, la composizione di morfismi permette di costruire nuove relazioni e funzioni in una categoria partendo da quelle esistenti, preservando la struttura e le operazioni interne della categoria.