La teoria delle categorie

La teoria delle categorie si occupa di oggetti e morfismi. Gli "oggetti" possono essere qualsiasi cosa, da insiemi a spazi, mentre i "morfismi" sono mappe che li connettono. Immagina gli oggetti come isole e i morfismi come ponti che li collegano. Questo quadro aiuta a comprendere come gli elementi matematici si relazionino l'uno con l'altro in modo strutturato e prevedibile.

Un esempio classico di categoria è quella degli insiemi, con gli insiemi stessi come oggetti e le funzioni come morfismi. Questa struttura base si estende a contesti più complessi come la categoria degli spazi vettoriali, dove gli oggetti sono spazi vettoriali e i morfismi sono trasformazioni lineari tra questi spazi.

La teoria delle categorie identifica strutture astratte comuni a diverse discipline, consentendo l'applicazione di soluzioni sviluppate in un campo del sapere alla risoluzione di problemi in un altro settore. Pur avendo origine nella matematica, promuove un approccio interdisciplinare, creando un linguaggio unificante tra diverse discipline. Questo permette, ad esempio, di utilizzare una soluzione informatica per affrontare un problema in fisica, o viceversa, ampliando significativamente le possibilità di collaborazione, innovazione e scoperta.

Cosa è una categoria?

Una categoria in matematica è un concetto astratto che include due elementi principali: oggetti e morfismi. Una categoria è definita dalle seguenti proprietà:

• Oggetti: Come accennato, possono essere qualsiasi cosa: insiemi, spazi topologici, gruppi, anelli, ecc.
• Morfismi: Sono le relazioni tra gli oggetti. Ogni morfismo ha un oggetto di origine e uno di destinazione e rappresenta una struttura di "freccia" che collega un oggetto all'altro.

Oltre a questi elementi, ci sono alcune regole che ogni categoria deve seguire:

• Identità: Ogni oggetto in una categoria ha un morfismo identità che mappa l'oggetto in sé stesso. Questo morfismo serve come elemento neutro per la composizione.
• Composizione: I morfismi possono essere composti in modo associativo. Se abbiamo morfismi \( f: A \rightarrow B \), \( g: B \rightarrow C \), e \( h: C \rightarrow D \), allora \( h \circ (g \circ f) = (h \circ g) \circ f \).

Le categorie sono fondamentali perché forniscono un framework unificante per trattare diverse strutture matematiche sotto un'unica teoria coesiva. Questo non solo permette di trasferire intuizioni e risultati tra diversi ambiti della matematica, ma aiuta anche a identificare e formalizzare analogie tra concetti altrimenti visti come separati.

Le categorie non sono solo di interesse puramente teorico. Hanno applicazioni pratiche in diversi campi della scienza e della tecnologia, in informatica, in fisica, nelle scienze in generale, ecc. Sono un potente strumento per la sintesi e l'analisi in molteplici discipline, permettendo di vedere oltre i dettagli specifici delle strutture individuali e di comprendere le relazioni fondamentali che le uniscono.

Gli oggetti, i morfismi e i diagrammi

Oltre alle categorie, la teoria delle categorie è strutturata attorno a tre componenti fondamentali: oggetti, morfismi e diagrammi.

Questi elementi collaborano per definire e esplorare le relazioni strutturali tra vari concetti matematici.

• Oggetti
  Gli oggetti sono i componenti fondamentali di una categoria. Possono rappresentare praticamente qualsiasi entità matematica, come insiemi, spazi, gruppi, anelli, ecc. In termini più astratti, gli oggetti sono i punti nodali tra cui i morfismi stabiliscono connessioni. Nonostante la loro diversità, gli oggetti all'interno di una categoria sono collegati da una struttura comune definita dai morfismi.
• Morfismi
  I morfismi, talvolta chiamati frecce o mappe, sono le relazioni tra gli oggetti in una categoria. Ogni morfismo ha un oggetto di partenza e un oggetto di arrivo. In matematica classica, un esempio di morfismo potrebbe essere una funzione che mappa elementi da un insieme (oggetto di partenza) a un altro (oggetto di arrivo). Importante è il concetto di composizione di morfismi: se esiste un morfismo da A a B e un altro da B a C, allora deve esistere un morfismo composito da A a C. La composizione deve essere associativa, e per ogni oggetto deve esistere un morfismo identità che mappa l'oggetto in sé stesso, fungendo da elemento neutro nella composizione.
  
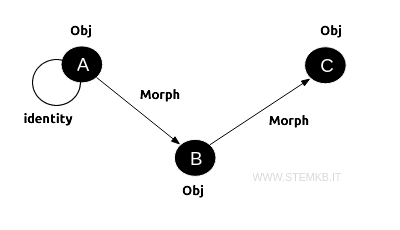
• Diagrammi
  I diagrammi nella teoria delle categorie aiutano a visualizzare le relazioni tra oggetti e morfismi. Un diagramma categorico è una rappresentazione grafica simile a un grafo orientato, dove gli oggetti sono indicati da nodi e i morfismi da frecce direzionate tra questi nodi. I diagrammi sono utili per esprimere condizioni come la commutatività, che indica che seguire percorsi diversi tra gli stessi oggetti nel diagramma porta allo stesso risultato. Questo aspetto è fondamentale per dimostrare l'equivalenza di espressioni matematiche diverse e per stabilire connessioni profonde tra strutture differenti.

Con questi fondamenti, la teoria delle categorie si rivela essere non solo un linguaggio descrittivo ma anche uno strumento di ricerca e innovazione.

Oltre a oggetti, morfismi e diagrammi, la teoria delle categorie include concetti più avanzati come i functori che sono mappe tra categorie che conservano la struttura di oggetti e morfismi, le trasformazioni naturali che descrivono le relazioni tra functori, i limiti e i colimiti che generalizzano i concetti di prodotti e coprodotti, che consentono di definire l'intersezione e l'unione in maniera categorica. Questi strumenti arricchiscono la teoria delle categorie, permettendo di esplorare in profondità la struttura interconnessa della matematica.

Un esempio

Un esempio molto chiaro è la categoria degli insiemi, comunemente indicata con il simbolo Set.

Vediamo come si articola questa categoria nei suoi elementi principali: oggetti e morfismi.

• Oggetti
  Nella categoria Set, gli oggetti sono tutti gli insiemi possibili. Questi possono variare da insiemi molto semplici, come insiemi finiti di numeri o lettere, a insiemi infiniti, come l'insieme dei numeri naturali o l'insieme dei punti su una linea.
• Morfismi
  I morfismi nella categoria Set sono tutte le possibili funzioni tra insiemi. Una funzione \( f \) da un insieme \( A \) a un insieme \( B \) (scritto matematicamente come \( f: A \rightarrow B \)) associa ogni elemento di \( A \) con un elemento di \( B \). La funzione deve essere ben definita, il che significa che ogni elemento di \( A \) ha esattamente un'immagine in \( B \).
• Composizione
  La composizione dei morfismi in Set segue la regola standard della composizione di funzioni. Se hai una funzione \( f: A \rightarrow B \) e un'altra funzione \( g: B \rightarrow C \), allora puoi comporre \( g \) con \( f \) per ottenere una nuova funzione \( g \circ f: A \rightarrow C \), che mappa ogni elemento di \( A \) in \( C \) passando per \( B \).
• Identità
  Ogni insieme in Set ha un morfismo identità, che è una funzione che mappa ogni elemento dell'insieme in se stesso. Per un insieme \( A \), il morfismo identità \( \text{id}_A: A \rightarrow A \) è la funzione definita da \( \text{id}_A(x) = x \) per ogni \( x \) in \( A \).

Ad esempio, considera tre insiemi: \( A = \{1, 2, 3\} \), \( B = \{a, b\} \), e \( C = \{x, y, z\} \).

Una possibile funzione \( f: A \rightarrow B \) potrebbe essere definita come:

$$  f(1) = a $$

$$  f(2) = a $$

$$  f(3) = b $$

Una possibile funzione \( g: B \rightarrow C \) potrebbe essere:

$$  g(a) = x $$

$$  g(b) = y $$

Possiamo rappresentare gli oggetti e i morfismi in un diagramma, dove le frecce indicano i morfismi.

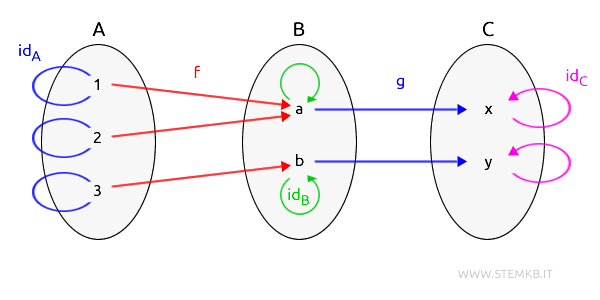
Questa configurazione di oggetti e di morfismi della categoria ci permette di costruire una composizione di morfismi $ g \circ f $.

La composizione \( g \circ f: A \rightarrow C \) risultante sarebbe:

$$ (g \circ f)(1) = g(f(1)) = g(a) = x $$

$$ (g \circ f)(2) = g(f(2)) = g(a) = x $$

$$ (g \circ f)(3) = g(f(3)) = g(b) = y $$

Oltre alle composizioni vanno considerati nella categoria Set anche i morfismi identità che mettono in relazione ogni oggetto con se stesso.

$$ id_A(1) = 1 \ \ \ id_A(2) = 2 \ \ \ id_A(3) = 3  $$

$$ id_B (a)=a \ \ \ id_B(b)=b $$

$$ id_C (x) = x \ \ \ id_C(y)=y $$

Questo esempio illustra come gli oggetti e i morfismi interagiscano nella categoria Set per formare una struttura coerente e come la composizione di funzioni crei nuove connessioni tra insiemi.