I criteri di congruenza dei triangoli

Due triangoli sono congruenti se hanno tutti i lati e tutti gli angoli corrispondenti uguali. In altre parole, sovrapponendoli, coincidono esattamente.

Per determinare se due triangoli sono congruenti, esistono alcuni criteri di congruenza, che ti consentono di verificare la loro uguaglianza senza dover misurare e confrontare direttamente tutti i lati e gli angoli.

Ecco quali sono i criteri di congruenza:

Criterio LAL (Lato-Angolo-Lato)

Due triangoli sono congruenti se hanno due lati uguali e l’angolo compreso tra essi uguale nello stesso ordine.

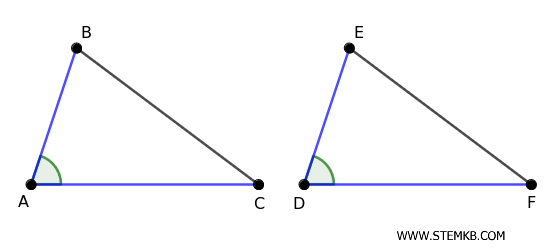
Ad esempio, immagina di avere due triangoli ABC e DEF, in cui due lati sono congruenti \( AB = DE \) e \( AC = DF \) e anche l'angolo compreso tra questi due lati è congruente \( \widehat{A} = \widehat{D} \).

Allora i due triangoli sono congruenti (\(\triangle ABC \cong \triangle DEF\)).

Se due case hanno le falde del tetto della stessa lunghezza e l’angolo di inclinazione del tetto uguale, allora possiamo essere certi che i due tetti sono identici. 

Criterio LLL (Lato-Lato-Lato)

Due triangoli sono congruenti se hanno tutti e tre i lati uguali.

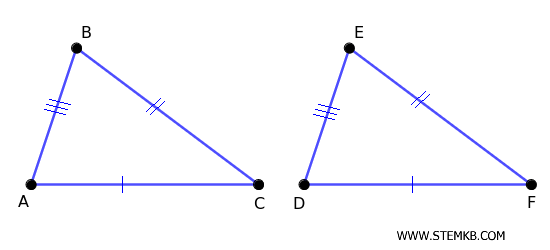
Ad esempio, supponi di avere due triangoli con tutti i lati congruenti \( AB = DE \), \( BC = EF \) e \( AC = DF \).

Allora i due triangoli sono congruenti (\(\triangle ABC \cong \triangle DEF\)).

Immagina di avere due case con le falde del tetto della stessa lunghezza e una trave orizzontale alla base di uguale lunghezza. Se tutte le misure coincidono, possiamo dire con certezza che i due tetti sono identici.

Criterio ALA (Angolo-Lato-Angolo)

Due triangoli sono congruenti se hanno un lato uguale e due angoli adiacenti uguali.

Se in due triangoli vedi un lato congruente \( AB = DE \), ossia della stessa lunghezza, e i due angoli adiacenti congruenti \( \widehat{A} = \widehat{D} \) e \( \widehat{B} = \widehat{E} \), allora i due triangoli sono congruenti (\(\triangle ABC \cong \triangle DEF\)).

 

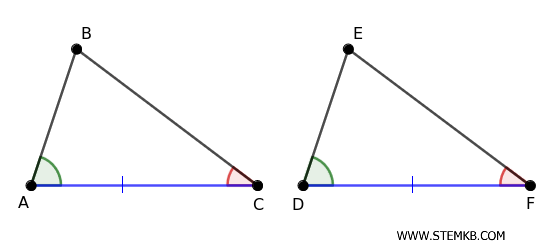
Supponiamo che due case abbiano la trave di base uguale e che gli angoli formati tra la trave orizzontale e le falde del tetto siano uguali. In questo caso, possiamo dire con certezza che le falde saranno uguali.

Criterio LAA (Lato-Angolo-Angolo)

Due triangoli sono congruenti se hanno un lato uguale e due angoli qualsiasi uguali.

Se in due triangoli c'è un lato congruente \( AB = DE \) e due angoli congruenti \( \widehat{A} = \widehat{D} \) e  \( \widehat{C} = \widehat{F} \), allora i due triangoli sono congruenti (\(\triangle ABC \cong \triangle DEF\)).

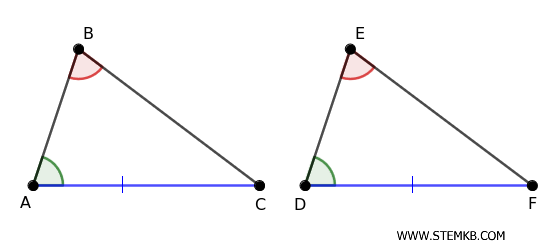
Se due case hanno la stessa lunghezza della falda e gli angoli di inclinazione del tetto sono uguali, possiamo essere certi che le due strutture siano identiche, anche senza conoscere la lunghezza della base.

Criterio di congruenza nei triangoli rettangoli

Per i triangoli rettangoli esistono due criteri specifici:

• Criterio Ipotenusa-Cateto (IC)
  Due triangoli rettangoli sono congruenti se hanno uguali l’ipotenusa e un cateto.

  Ad esempio, se in due triangoli rettangoli \( ABC \) e \( DEF \) hai l'ipotenusa \( BC = EF \) e un cateto \( AC = DF \) ( oppure \( AB = DE \) ) congruente, allora i due triangoli rettangoli sono congruenti\( \triangle ABC \cong \triangle DEF \).
  

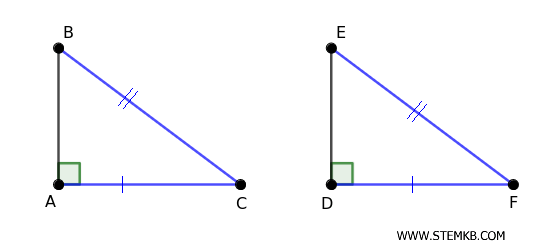
• Criterio Cateto-Cateto (CC)
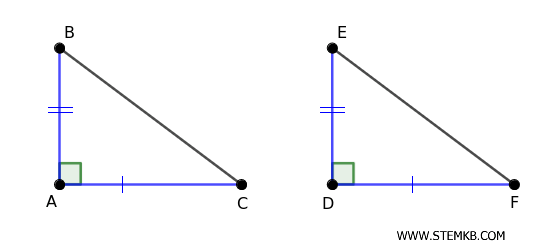
  Due triangoli rettangoli sono congruenti se hanno uguali entrambi i cateti.

  Ad esempio, se in due triangoli rettangoli \( ABC \) e \( DEF \) i cateri \( AC = DF \) e \( AB = DE \) sono congruenti, allora \( \triangle ABC \cong \triangle DEF \).
  

In conclusione, icriteri di congruenza ti permettono di verificare rapidamente se due triangoli sono uguali senza dover misurare tutti i loro elementi.

Tutti questi principi sono essenziali in geometria, perché puoi trovarli in moltissime dimostrazioni.