Incentro
L’incentro di un triangolo è il punto in cui si incontrano le tre bisettrici degli angoli interni del triangolo. È un punto speciale perché è anche il centro del cerchio inscritto, ovvero il cerchio che è tangente a tutti e tre i lati del triangolo.
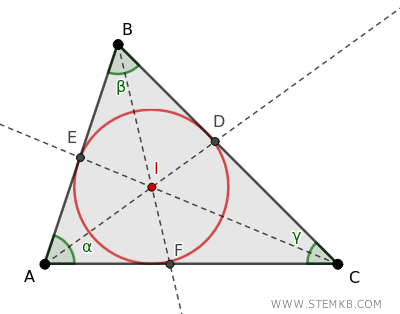
Immagina di avere un triangolo qualsiasi, magari disegnato su un foglio di carta.
Ora, prova a pensare a un punto speciale dentro questo triangolo: un punto che sia equidistante da tutti i suoi lati. Questo punto esiste ed è chiamato incentro.
L’incentro è uno dei punti notevoli più importanti del triangolo. Non solo è il punto di incontro delle bisettrici, ma è anche il centro del cerchio inscritto e ha proprietà geometriche molto utili.
Ma come facciamo a trovarlo? E perché ha questa proprietà così interessante? Facciamolo passo dopo passo, con un approccio semplice e intuitivo.
Le bisettrici sono la chiave per trovare l’incentro
Per scoprire dove si trova l’incentro, dobbiamo tracciare le bisettrici degli angoli del triangolo. Una bisettrice è una linea che divide un angolo in due parti uguali.
Prendi un triangolo qualsiasi e scegli uno degli angoli. Usa un goniometro per misurare l’angolo e dividilo in due parti uguali.
Poi traccia una linea che passi per il vertice e tagli l’angolo in due parti uguali. Hai appena disegnato una bisettrice.
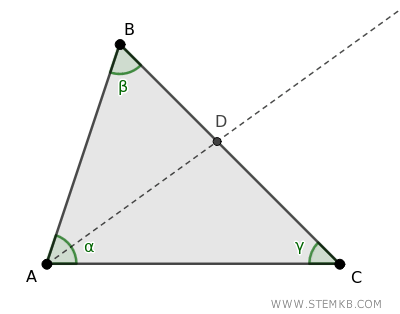
Fai lo stesso per gli altri due angoli del triangolo. Noterai che tutte e tre le bisettrici si incontrano in un unico punto \( I \): quello è l’incentro!
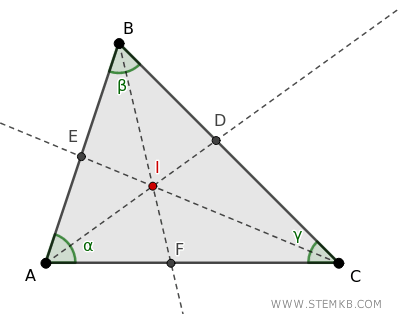
Perché l’incentro è speciale?
L’incentro ha una proprietà molto interessante: è il punto che dista esattamente la stessa misura da tutti e tre i lati del triangolo.
Questo significa che, se prendi un compasso e lo metti con la punta sull’incentro, puoi disegnare un cerchio che tocca perfettamente tutti e tre i lati. Questo cerchio si chiama cerchio inscritto.

Immagina una situazione concreta. Se hai un campo triangolare e vuoi costruire una fontana in un punto equidistante da tutti i tre lati del campo (per esempio, perché vuoi che l'acqua sia facilmente raggiungibile da ogni lato), allora dovrai costruirla proprio nell’incentro del triangolo.
L’incentro cambia con il triangolo?
Una proprietà particolare dell’incentro è che si trova sempre dentro il triangolo, indipendentemente dal tipo di triangolo che hai.
A seconda del tipo di triangolo può cambiare solo la sua posizione.
Ad esempio, se il triangolo è acutangolo (cioè con tutti gli angoli minori di 90°), l’incentro sarà più o meno al centro. Se il triangolo è rettangolo, l’incentro si sposta un po’ più vicino all’angolo retto. Infine, se il triangolo è ottusangolo (cioè ha un angolo maggiore di 90°), l’incentro sarà più vicino al lato opposto all’angolo più grande.
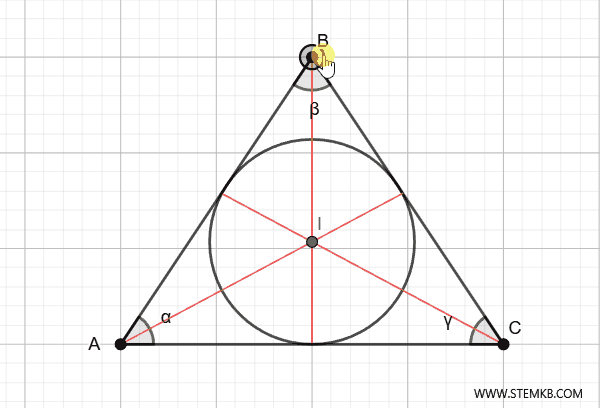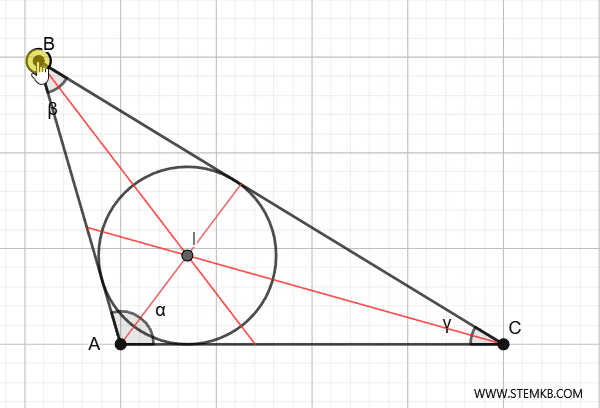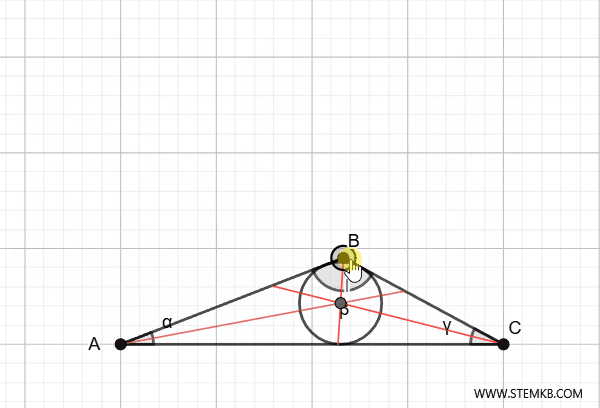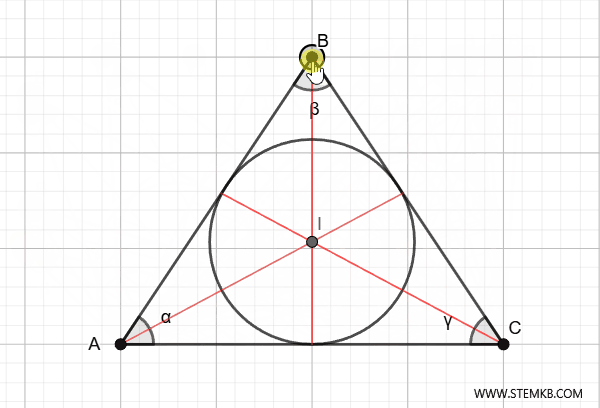
La prossima volta che disegni un triangolo, prova a trovare il suo incentro! Ti accorgerai di quanto sia un punto speciale, sia geometricamente che concettualmente.