Le bisettrici di un triangolo
Una bisettrice di un triangolo è un segmento che divide un angolo interno del triangolo in due angoli uguali e termina sul lato opposto.
Immagina di avere un triangolo. Prendi uno degli angoli interni, ad esempio l'angolo alfa, e traccialo a metà, come se dividessi una fetta di pizza in due parti uguali.
Il segmento AD che hai appena disegnato si chiama bisettrice.
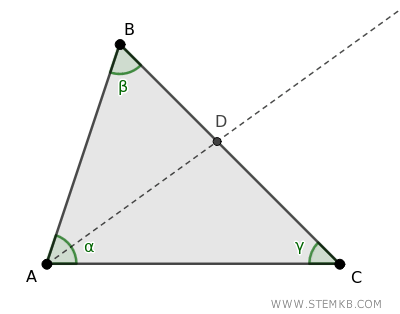
Ora, ogni triangolo ha tre angoli, quindi puoi tracciare tre bisettrici interne.
La cosa sorprendente è che queste tre bisettrici si incontrano tutte nello stesso punto! Questo punto magico si chiama incentro.
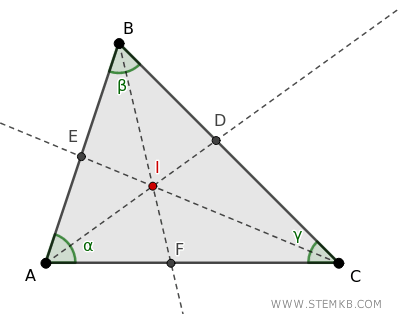
Ma a cosa serve l’incentro? Beh, è il centro del cerchio inscritto, cioè il cerchio che si incastra perfettamente dentro il triangolo, toccando tutti e tre i lati senza mai uscire. In altre parole, il cerchio è tangente a tutti e tre i lati del triangolo.
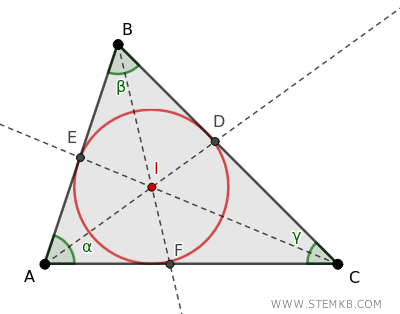
La proprietà di divisione dei lati delle bisettrici
La bisettrice non è solo un semplice segmento che divide un angolo a metà. Fa anche un altro lavoro interessante: quando arriva al lato opposto, lo divide in due segmenti proporzionali agli altri due lati del triangolo.
In parole povere, se chiamiamo queste due parti \(m\) e \(n\), e i due lati del triangolo che formano l’angolo \(a\) e \(b\), allora vale questa regola:
\[ \frac{m}{n} = \frac{a}{b} \]
È come dire che la bisettrice ha una sorta di "equilibrio naturale", mantenendo le proporzioni tra i lati.
Facciamo un esempio pratico.
In questo triangolo la bisettrice dell'angolo \( \beta \) divide il lato opposto in due parti $ m $ e $ n $.
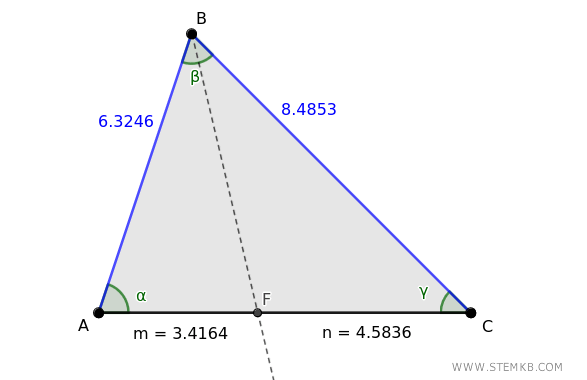
Il rapporto tra le lunghezze dei segmenti $ m $ e $ n $, quello minore fratto quello maggiore, è circa 0.7454
$$ \frac{m}{n} = \frac{3.4164}{4.5836} = 0.7454 $$
Anche il rapporto tra i lati \( AB \) e \( BC \) che formano l'angolo \( beta \) è 0.7454, ponendo al numeratore sempre il lato minore.
$$ \frac{AB}{BC} = \frac{6.3246}{8.4853} = 0.7454 $$
Questa proprietà vale per tutte le bisettrici del triangolo.
Le bisettrici esterne
Oltre alle bisettrici interne, esistono anche le bisettrici esterne, che invece di dividere un angolo interno, dividono a metà un angolo esterno del triangolo.
Se prendi due bisettrici esterne di due angoli distinti e la bisettrice interna del restante angolo, vedrai che si incontrano in un punto che sta fuori dal triangolo. Questo punto si chiama excentro.
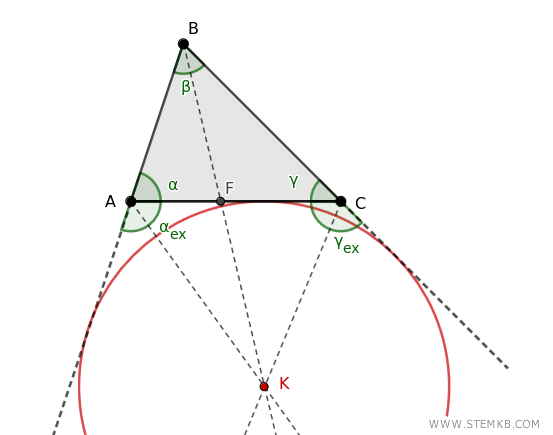
E che fa l’excentro? È il centro di un altro cerchio speciale: il cerchio ex-inscritto, che è un cerchio tangente a un lato del triangolo e ai prolungamenti degli altri due.
Insomma, è il cugino del cerchio inscritto, ma più "esterno".