L'ortocentro
L'ortocentro è il punto in cui si incontrano le altezze del triangolo.
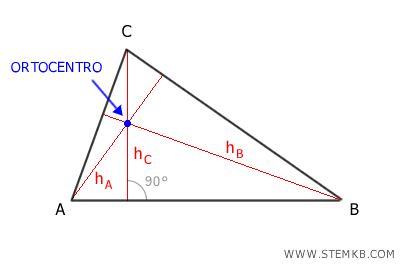
Dove un'altezza del triangolo è un segmento di linea che va da un vertice del triangolo al lato opposto o al suo prolungamento e che è perpendicolare a quel lato.
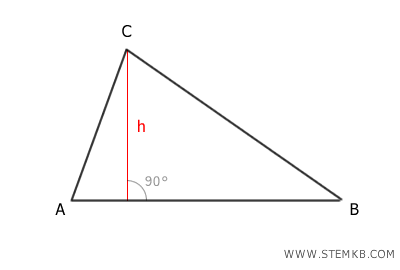
Per capire meglio di cosa si tratta, disegna tutte le altezze del triangolo.
Ce ne sono tre, una per ogni vertice e lato. Sono i segmenti hA, hB, hC.
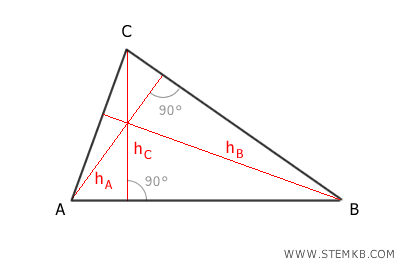
Come puoi vedere, le tre altezze del triangolo si intersecano tutte in un unico punto. Quel punto è l'ortocentro.

Si tratta di un punto particolare (o punto notevole) del triangolo e ha proprietà uniche e interessanti.
L'ortocentro può trovarsi all'interno, sull'ipotenusa in caso di triangoli rettangoli, o all'esterno del triangolo nel caso di triangoli ottusangoli.
Se stai lavorando su problemi legati all'ortocentro, può essere utile disegnare dei triangoli diversi (acutangoli, rettangoli, ottusangoli) e costruire le relative altezze per trovare l'ortocentro. Questo può aiutare a comprendere meglio la sua posizione in relazione ai vari tipi di triangoli.
Ad esempio, in un triangolo acutangolo, ovvero con tutti gli angoli interni inferiori a 90°, l'ortocentro si trova all'interno del triangolo.
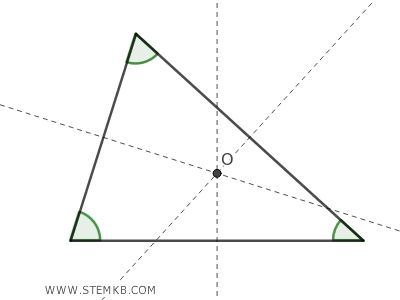
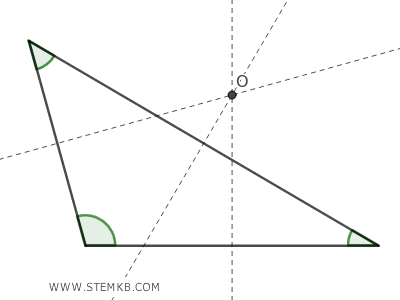
In un triangolo ottusangolo, quello con un angolo superiore a 90°, l'ortocentro si trova all'esterno del triangolo.
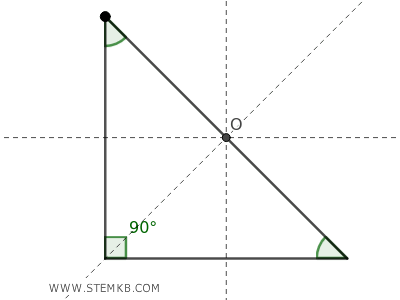
In un triangolo rettangolo, invece, l'ortocentro corrisponde al vertice dell'angolo retto.
La relazione tra l'ortocentro e gli altri punti notevoli del triangolo. Una curiosità interessante che lega tra loro tutti i punti notevoli del triangolo. L'ortocentro, il baricentro, il circocentro e l'incentro di un triangolo sono sempre allineati su una stessa retta, nota come linea di Eulero. Inoltre, nel caso particolare del triangolo equilatero, l'ortocentro coincide con il baricentro, il circocentro e l'incentro, ovvero con gli altri punti notevoli del triangolo.