Il punto medio di un segmento
Cos'è il punto medio di un segmento?
Un segmento è una linea retta delimitata da due punti estremi, che chiameremo \( A \) e \( B \).

Il punto medio è il punto che si trova esattamente al centro del segmento, dividendolo in due parti uguali o, come si dice in termini matematici, in due segmenti "congruenti".
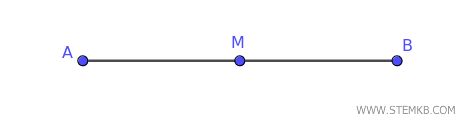
In altre parole, se il punto medio è \( M \), allora \( AM = MB \).
Questa definizione è più di una semplice proprietà geometrica: il punto medio rappresenta anche un concetto di equilibrio e simmetria. Lo troviamo spesso in applicazioni reali, come nella progettazione di strutture o nella suddivisione equa di spazi e risorse.
Come si trova il punto medio?
Per determinare il punto medio di un segmento, la procedura varia leggermente a seconda del contesto:
1] Su una retta numerica
Supponiamo che i punti \( A \) e \( B \) abbiano coordinate rispettivamente \( x_1 \) e \( x_2 \) su una retta. Il punto medio si trova calcolando la media aritmetica delle coordinate:
$$ M = \frac{x_1 + x_2}{2} $$
Ad esempio, prendiamo un segmento $ AB $ su una linea che ha per estremi i punti \( A = 2 \) e \( B = 8 \).
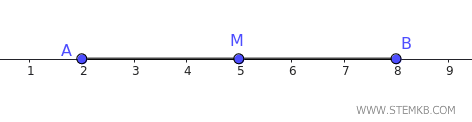
Poi calcoliamo il punto medio
$$ M = \frac{2 + 8}{2} = 5 $$
Il punto medio si trova nel punto $ M= 5 $ della linea, esattamente alla metà del segmento.

Come puoi notare, il punto $ M $ è equidistante dagli estremi $ A $ e $ B $ del segmento.
Ha diviso il segmento $ AB $ in due segmenti $ AM $ e $ MB $ che hanno la stessa lunghezza $ AM=MB $, ovvero sono "congruenti".
$$ AM \cong MB $$
Due segmenti si dicono congruenti se è possibile sovrapporli esattamente punto per punto, senza che rimangano parti scoperte..
2] Nel piano cartesiano
Se i punti \( A \) e \( B \) hanno coordinate \( (x_1, y_1) \) e \( (x_2, y_2) \), il punto medio si calcola considerando sia le coordinate \( x \) che quelle \( y \):
$$ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) $$
Ad esempio, ipotizziamo di avere due punti alle coordinate \( A(2, 3) \) e \( B(8, 7) \).
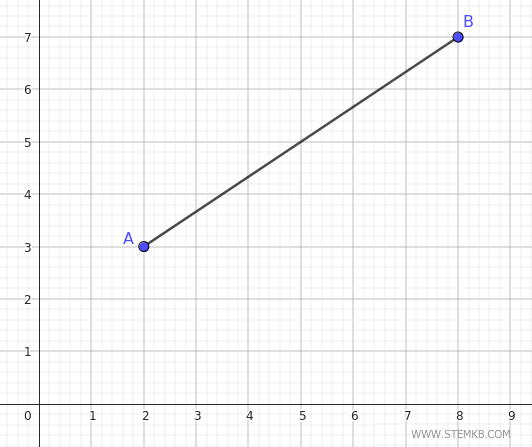
Per trovare il punto medio $ M $, dobbiamo calcolare la media delle componenti x e y delle coordinate dei punti.
$$ M = \left( \frac{2+8}{2}, \frac{3+7}{2} \right) = (5, 5) $$
Quindi, il punto medio $ M $ del segmento si trova alle coordinate $ (5,5) $ del piano.
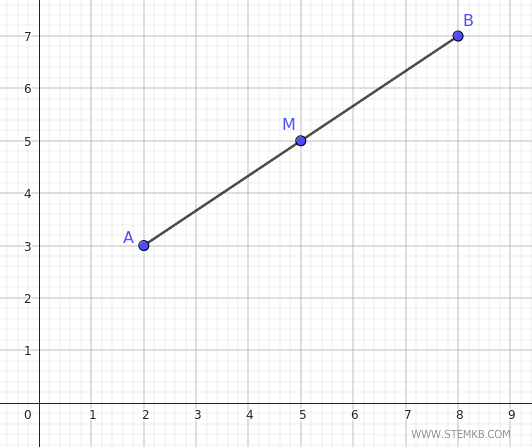
Anche in questo caso il punto medio $ M = ( 5,5 ) $ si trova esattamente alla metà del segmento $ AB $, è equidistante dai due estremi $ A $ e $ B $.
I segmenti $ AM $ e $ MB $ hanno la stessa lunghezza, sono congruenti.
$$ AM \cong MB $$
Trovare il punto medio di un segmento ci insegna che spesso, nel mezzo, si nasconde un equilibrio perfetto.