ll complemento di un grafo
Il complemento di un grafo consiste in un grafo che conserva gli stessi vertici di quello originale, ma la presenza dei lati è invertita: nel grafo complemento due vertici sono uniti da un arco se e solo se non lo erano nel grafo originale.
Formalmente il complemento \( \bar{G} \) di un grafo \( G \) è un altro grafo composto dagli stessi vertici $ V(G) $ e dai lati $ uv \in \bar{E}(G) $ che non sono presenti nel grafo d'origine $ uv \notin E(G) $.
In altre parole, il complemento di un grafo ha le connessioni opposte rispetto al grafo originale.
Se due vertici non sono connessi da un lato nel grafo $ G $, allora sono connessi nel complemento \( \bar{G} \) e viceversa.
Il complemento di un grafo è una specie di immagine speculare rispetto alle connessioni tra i vertici del grafo iniziale. Una sorta di grafo "allo specchio".
Esempio
Immaginiamo una festa con alcuni ospiti e un grafo che rappresenta chi conosce chi. Ogni persona è un punto (vertice) e disegniamo una linea (spigolo) tra due persone se si conoscono.
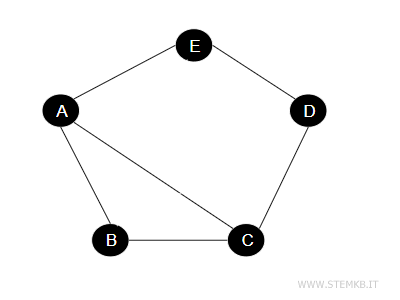
Se ora vogliamo creare un "anti-grafo" della festa, che mostra invece chi NON conosce chi, prendiamo gli stessi punti (vertici), ma questa volta disegniamo una linea tra due persone solo se queste non si sono mai incontrate.
Quindi, ogni coppia di persone che non aveva una linea tra loro nel primo grafo, adesso ne avrebbe una nel secondo, e viceversa.
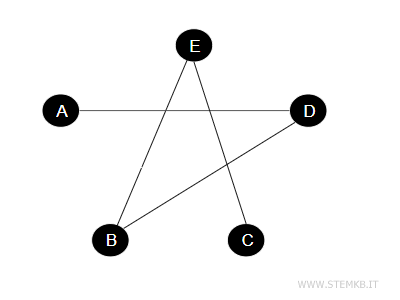
Questo "anti-grafo" è quello che chiamiamo il complemento del grafo originale. In pratica, il complemento di un grafo ci mostra tutte le connessioni mancanti del grafo originale.
Merita d'essere sottolineato che l'unione di un grafo \(G\) con il suo complemento \( \bar{G} \) dà come risultato un grafo completo. Questo perché, per definizione, in \(G\) ci sono alcuni archi che collegano certi vertici, mentre nel suo complemento \( \bar{G} \), ci sono archi che collegano tutti i vertici che non sono collegati in \(G\). Unendo \(G\) e \( \bar{G} \), finiamo per avere un arco tra ogni coppia di vertici, che è proprio la definizione di un grafo completo. In un grafo completo, ogni vertice è collegato direttamente a ogni altro vertice, senza eccezioni.
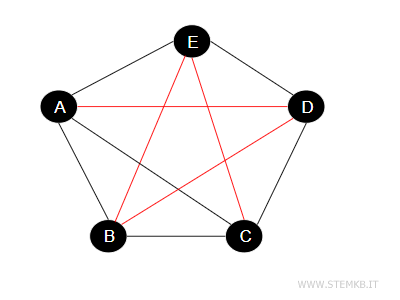
Il complemento di un grafo permette di studiare le proprietà di un grafo esaminando il suo complemento.
A volte, è più facile analizzare certe caratteristiche del complemento di un grafo piuttosto che del grafo stesso.
Inoltre, in alcuni problemi di ottimizzazione, come il problema del massimo clique o del massimo insieme indipendente, lavorare con il complemento di un grafo può semplificare l'approccio o rendere più efficienti gli algoritmi.
Ad esempio, la ricerca di un insieme indipendente massimale in un grafo è equivalente alla ricerca di un clique massimale nel suo complemento.
Domande/Risposte
- Il complemento di un grafo completo è un grafo vuoto?
E' vero. Un grafo completo ha un arco tra ogni coppia di vertici, quindi non ci sono coppie di vertici non connesse che possono essere collegate nel complemento. Pertanto, il complemento non avrà archi, rendendolo un grafo vuoto. - Il complemento di un grafo bipartito è un grafo connesso?
Questa affermazione non è necessariamente vera. Il complemento di un grafo bipartito può essere connesso o non connesso, a seconda della struttura specifica del grafo bipartito. Ad esempio, se ogni vertice in un insieme del grafo bipartito è connesso ad almeno un vertice nell'altro insieme, il complemento sarà connesso. Tuttavia, se ci sono vertici che non sono connessi a nessun vertice dell'altro insieme, il complemento può risultare in più componenti connesse. - Il complemento di un grafo connesso può essere non connesso?
Questo è vero. Considera un grafo semplice a forma di anello, dove ogni vertice è connesso solo ai suoi due vicini più prossimi. Il grafo è chiaramente connesso. Tuttavia, il suo complemento disconnetterà questi vertici in modo tale che non ci sia un cammino tra alcuni di essi, rendendo il complemento non connesso. - Il complemento di un grafo con un numero pari di lati è un grafo bipartito?
Questa affermazione non è generalmente vera. La proprietà di essere bipartito non dipende dal numero di archi nel grafo, ma piuttosto dalla possibilità di dividere l'insieme dei vertici in due sottogruppi tali che non ci siano archi che collegano vertici all'interno dello stesso sottogruppo. Il numero di archi (pari o dispari) non determina se il complemento sarà bipartito.