Il numero cromatico dei vertici in un grafo
Il numero cromatico $ \chi(G) $ di un grafo G = (V, E) è il minimo numero di colori necessario per colorare i vertici del grafo in modo tale che nessun vertice adiacente abbia lo stesso colore.
In altre parole, è il numero minimo di colori che garantisce che non ci siano due vertici "vicini" con lo stesso colore.
Una colorazione del grafo G è una funzione f: V → C che assegna un colore ad ogni vertice.
Il numero cromatico di G si indica con χ(G) ed è il minimo numero di colori necessari per una colorazione valida del grafo.
Calcolare il numero cromatico di un grafo può rivelarsi un compito complesso dal punto di vista computazionale. Esistono vari algoritmi volti a stimare o identificare il numero cromatico. Tuttavia, per certi grafi, il problema della colorazione si classifica come NP-completo.
Esempio
Ad esempio, in questo grafo bipartito il numero cromatico del grafo è $ \chi(G) = 2 $.
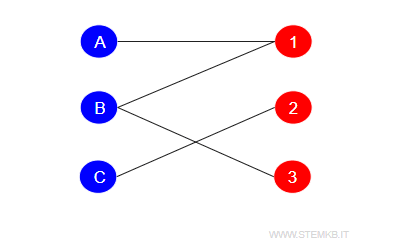
Si può notare che nel grafo precedente nessun vertice è adiacente a un altro vertice con lo stesso colore.
Dove per "vertice adiacente" si intende un vertice direttamente collegato con uno spigolo a un altro vertice.
Nel contesto dei grafi bipartiti il numero cromatico dei vertici è sempre 2, poiché per definizione non esistono spigoli che collegano due vertici all'interno dello stesso insieme. Quindi, è possibile colorare tutti i vertici di un insieme indipendente con lo stesso colore.
Esempio 2
Per fare un esempio di un grafo che richiede 3 colori per essere colorato in modo che nessun due vertici adiacenti abbiano lo stesso colore, possiamo utilizzare il grafo del triangolo, noto anche come \(C_3\), un ciclo semplice su 3 vertici.
Questo è uno dei grafi più semplici tra quelli non bipartiti.
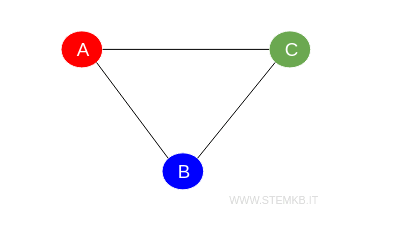
In questo caso il numero cromatico del grafo è $ \chi(G) = 3 $.
Per colorare questo grafo, abbiamo bisogno di 3 colori diversi perché ogni vertice è adiacente a tutti gli altri vertici.
L'assegnazione dei colori potrebbe essere: A-rosso, B-Blu, C-Verde. Questo assicura che ogni vertice adiacente abbia colori diversi.
Esempio 3
Questo è un altro esempio di grafo con numero cromatico $ \chi(G) = 3 $
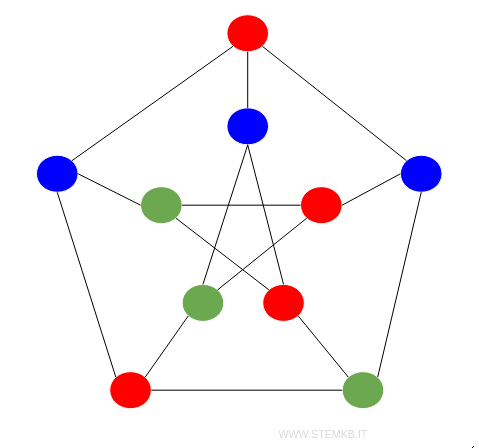
Anche in questo caso tutti i vertici adiacenti hanno un colore diverso.
Quali sono le applicazioni del numero cromatico
Il numero cromatico ha diverse applicazioni in vari campi.
In cartografia è utilizzato per la colorazione di mappe in modo da evitare confusione tra regioni adiacenti.
Può essere impiegato anche nella teoria della computazione per l'analisi di algoritmi o nella risoluzione di problemi di scheduling e di assegnazione di risorse.
Domande/Risposte
- Se un grafo è bipartito il suo numero cromatico è 2?
Sì, se un grafo è bipartito, il suo numero cromatico è 2. Questo perché è possibile colorare tutti i vertici di uno dei due insiemi con un colore, e tutti i vertici dell'altro insieme con un secondo colore, garantendo che nessun due vertici adiacenti abbiano lo stesso colore. - Un grafo con numero cromatico k è sempre detto k-partito?
No, il concetto di grafo k-partito e il numero cromatico $ \chi{(G)} $ di un grafo sono relazionati ma non identici, e un grafo con numero cromatico $ \chi{(G)}=k $ non è necessariamente detto k-partito. - Il numero cromatico di un grafo con n vertici è sempre compreso tra 1 e n?
Sì, l'affermazione è corretta: il numero cromatico di un grafo con \(n\) vertici è sempre compreso tra 1 e \(n\). Il minimo (1) si ha quando il grafo è completamente disconnesso, permettendo di colorare tutti i vertici con lo stesso colore. Il massimo (\(n\)) si verifica in un grafo completamente connesso, dove ogni vertice deve avere un colore diverso per soddisfare la regola che vertici adiacenti abbiano colori diversi. - Il numero cromatico di un grafo con un ciclo dispari è almeno 3?
Si, la presenza di un ciclo dispari in un grafo impedisce che il grafo possa essere colorato con soli 2 colori, quindi il numero cromatico deve essere almeno 3. Questo accade perché il più piccolo ciclo di lunghezza dispari è composto da tre vertici connessi tra loro a triangolo. In un triangolo, dopo aver colorato due vertici adiacenti con due colori diversi, non c'è modo di colorare il terzo vertice senza ripetere uno dei colori usati, perché è adiacente a entrambi i vertici già colorati.
